Viability Envelopes This page illustrates examples of application of viability envelopes; for particulars of the method please see our ICRA2004 paper. Also available are the ICRA 2004 talk slides, or Powerpoint slides of the DGP Research day talk. Abstract This work presents a numerical method for the containment of the state of a dynamic system within some arbitrarily shaped region of state-space. One such useful region, as employed in all the examples, is the subject's vability region, the set of all states in which the subject is controllable. Containment is achieved by constraining the allowed control inputs. The region can be specified externally, or in the case of viability, may be automatically discovered (further details here). Application to simple vehicle motion is shown.

Example: vertical rocket

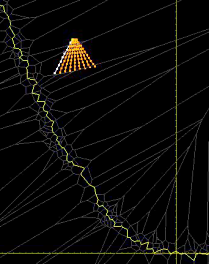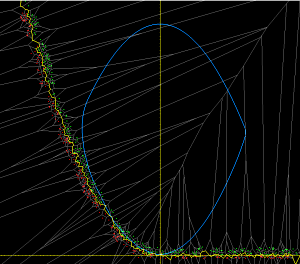
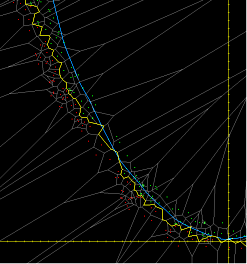
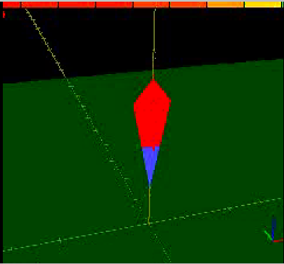
A vertical axis rocket that is constrained using a viability envelope to avoid collision with the ground.

Legend for the state-space view:

• green & red dots: sample rocket states which are known to be viable(green) and non-viable(red); their non-uniform placement is a result of the stochastic nature of the process used to obtain them
• grey lines: the Voronoi regions defined by the above samples
• yellow line: the decision surface (i.e., the approximation of the viability envelope derived from the above sample set)
• blue curve: the rocket's trajectory in the movie
• orange "rake": the set of short-term simulations performed by the system to gauge which control inputs are viable; the white line indicates the control input chosen

Legend for the world-space view:

• blue "tail" on rocket: indicates amount of thrust being applied (i.e., the control input)
• color bar across top: display of the tested control inputs and their "time to envelope breach"; red indicates 0s, green indicates the time is equal or larger than the "time horizon"; the inputs across the top are varying amounts of (constant) thrust, with zero thrust on left, and full thrust on right

Example: car

In this example we have a car constrained to a viability envelope for a rectangular track, while the user applies a roughly sinusoidal control input (steering angle).

This is a plot of user's control input (red), final applied control input (blue), and the unviability of particular control inputs at various points in time (pale green). In essence the system tries to track the user's (red) control input, except when it is unviable (pale green region). Click on the plot for a full size image of the plot.

The corresponding world-space view of the run is shown below, on the left, while on the right is the viability envelope (click for movie):

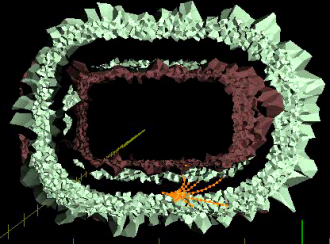Below is another car example, in a different terrain:

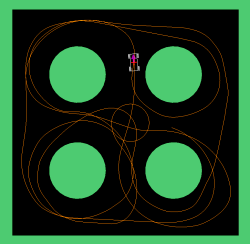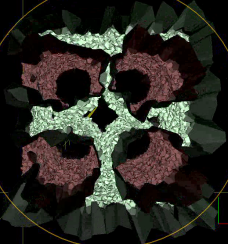example: bike

Finally here is an example of a bike under viability envelope constraint. The envelope ensures the bike does not fall over.

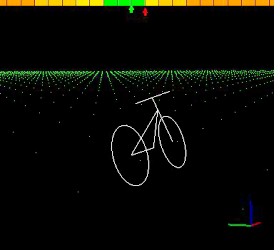In the world-space view of the bike, in the color/viability bar at top, the red arrow indicates the control input being requested by the user, while the green arrow indicates the control input actually applied. The cell color for the various control inputs at top is same as in the rocket scenario. In this example the control input consists of the steering angle, as well as the forward velocity, hence why the viability envelope is embedded in the 3D space: (lean, dlean/dt, forward velocity).

Movies

The remaining is a quick dump of all movies created. Please note that these are "raw", unaltered movies obtained in the course of research, and as such are neither polished nor as clear and helpful as they could be.

• all movies
• movie: rocket landing using analytic envelope; of note is how exact the system is, despite the control input space having been discretized to only 9 values. The lights at the top indicate proximity of a breach (red = breached immediate, green = no breach in time horizon). The two tiny arrows below them indicate the user's input (red arrow), and the final applied input (green arrow). Left end is 0 thrust, right is max thrust.
• movie: rocket landing using approximate envelope; here the user applies full thrust for an initial period, then cuts power to 0% for the remainder of the run.
• movie: state-space view of same run. The red and green points are the "out" and "in" samples that give rise to the viability envelope (jagged yellow line) using a Nearest Neighbour classifier. The orange tree is the set of trajectories of the system for the various candidate control inputs. The white one is the one curretly adopted by the system (only shown if applied input is from the discrete set).
• movie: a closer look at the state-space behaviour; note that the x and y axes have been swapped.
• movie: bike balancing using a viability envelope; note that although only the steering angle is being monitored and corrected, the user is allowed full freedom in controlling the bike's velocity. In the future we plan to look at performing corrections in such multi-dimensional control input spaces explicitly.
• movie: the state-space behaviour of a car's state; this introduces the simplified "car on straight road" model, where the state-space consists of car's orientation plotted on y axis vs the car's displacement from the middle of the road in the x axis.
• movie: the same car being contained within the envelope for this scenario. This was our first testcase and uses a hand generated polygonal envelope instead of the typical NN one.
• movie: car on a rectangular track under envelope containment; the purple arrow indicates the difference between the applied input and the user's originally requested input.
• movie: the 3D envelope in state-space for the above example
• movie: a more unconventional terrain for the car; symmetry was used purely for aesthetic reasons, and is not necessary
• movie: the 3D envelope in state-space for the above example