Spatio-Spectral Concentration on the Sphere

Christian Lessig and Eugene Fiume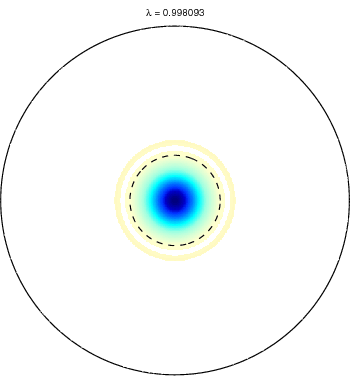




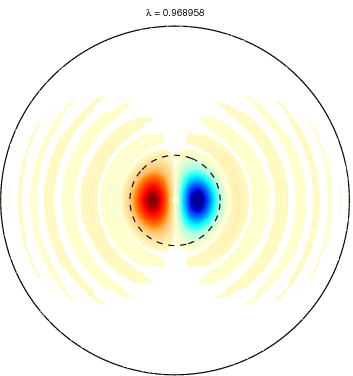
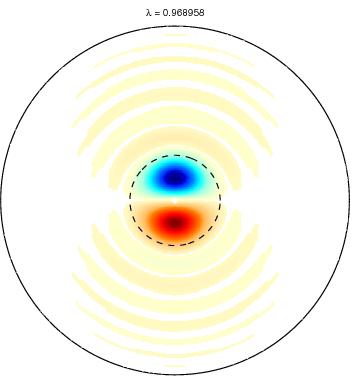
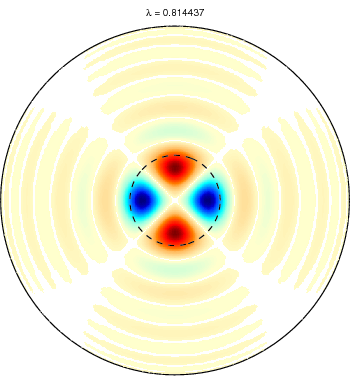
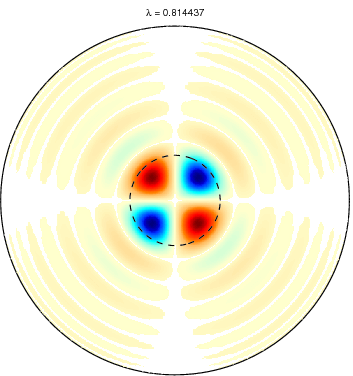
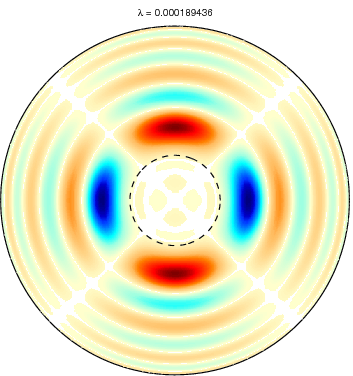
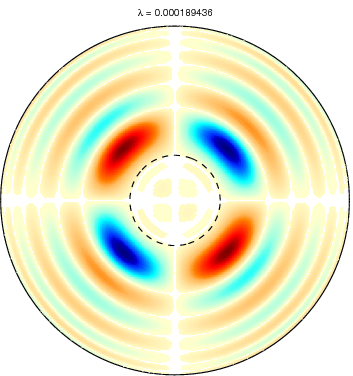
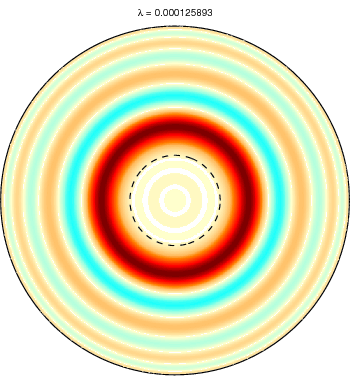
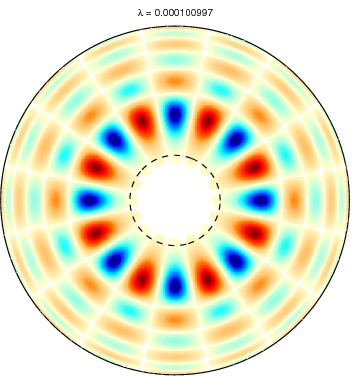
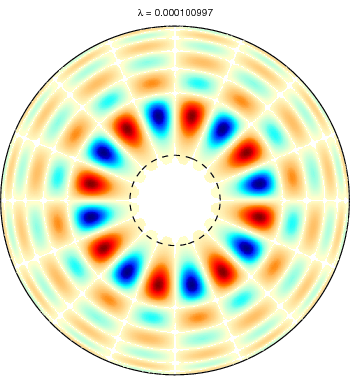
Spherical Slepian functions for L = 20 and a spherical cap with θ ≤ 15 degree (dotted circle). The first row shows the first five Slepian functions corresponding to the five largest eigenvalues and the second row Slepian functions with the corresponding eigenvalues very close to zero. Positive values are shown in blue and negative values in red. Very small values are left white.

Abstract: Spatio-spectral concentration theory is concerned with the optimal space localization of a signal bandlimited in the frequency domain. The question was first considered in a series of classic papers by Slepian, Pollak, and Landau [1961; 1961; 1962; 1978] who studied the problem on the real line; an introduction to the early work on the subject can be found in two articles by Slepian [1976; 1983]. Recently, Simons and co-workers [2006; 2009; 2010b] extended these results to the sphere. We present a concise and self-contained introduction to spatio-spectral concentration theory.

See also our paper on the effective dimension of light transport in a local neighborhood where we use Slepian functions.

Technical Report

Christian Lessig and Eugene Fiume, Spatio-Spectral Concentration on the Sphere, Technical Report, University of Toronto. (preprint)

Miscellaneous

Source code will be available shortly. Please send us a note if you need it urgently.

Acknowledgement

We thank Tyler de Witt and Jos Stam for helpful discussion. The implementation of Slepian functions by Frederik Simons was also valuable for our research.

May 2010