A Dirac Operator for Extrinsic Shape Analysis SGP 2017

Hsueh-Ti Derek Liu¹, Alec Jacobson², Keenan Crane¹

¹Carnegie Mellon University, ²University of Toronto

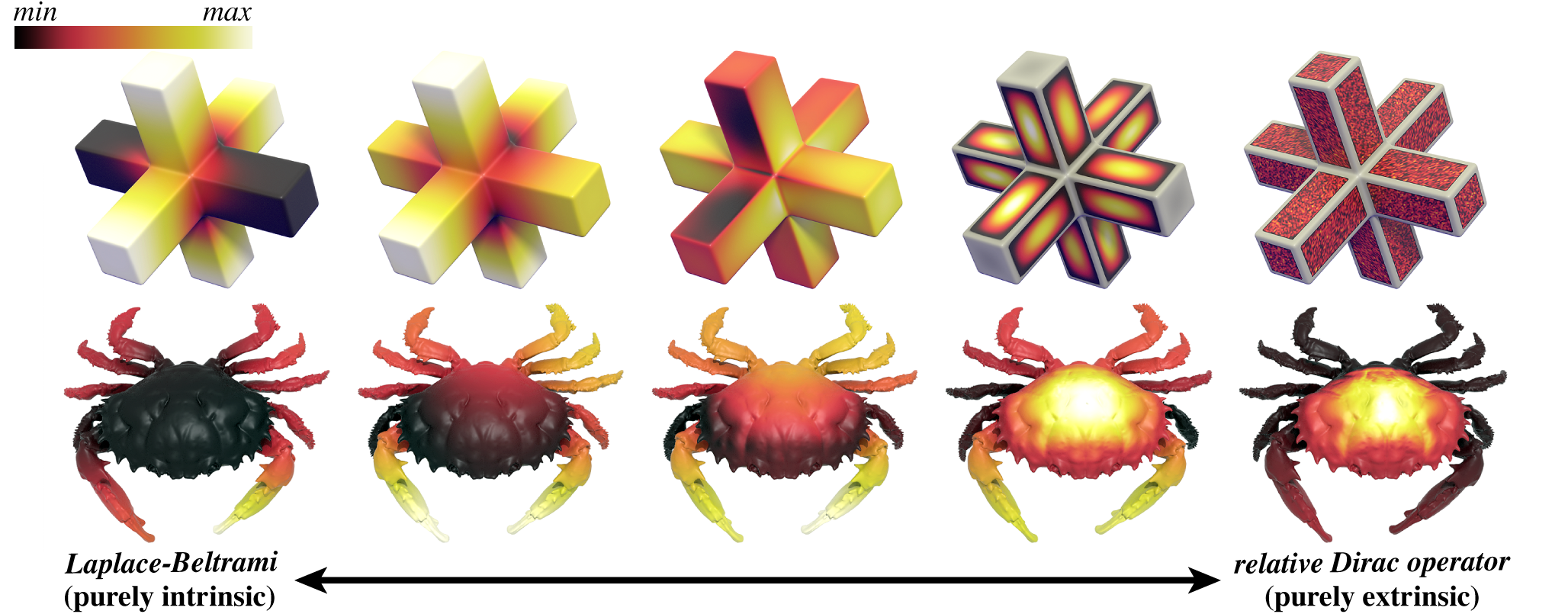
Not all differential operators encode the same information about shape. Here we visualize eigenfunctions of Laplace-Beltrami (left) which ignores extrinsic bending, and our relative Dirac operator (right) which ignores intrinsic stretching. In between is a continuous spectrum of operators that provide a trade off between intrinsic and extrinsic features. Bottom: These operators yield very different shape descriptors, here emphasizing either a pointy claw with large Gauss curvature (left) or the flat back of a shell with small mean curvature (right).
Not all differential operators encode the same information about shape. Here we visualize eigenfunctions of Laplace-Beltrami (left) which ignores extrinsic bending, and our relative Dirac operator (right) which ignores intrinsic stretching. In between is a continuous spectrum of operators that provide a trade off between intrinsic and extrinsic features. Bottom: These operators yield very different shape descriptors, here emphasizing either a pointy claw with large Gauss curvature (left) or the flat back of a shell with small mean curvature (right).

Abstract

The eigenfunctions and eigenvalues of the Laplace-Beltrami operator have proven to be a powerful tool for digital geometry processing, providing a description of geometry that is essentially independent of coordinates or the choice of discretization. However, since Laplace-Beltrami is purely intrinsic it struggles to capture important phenomena such as extrinsic bending, sharp edges, and fine surface texture. We introduce a new extrinsic differential operator called the relative Dirac operator, leading to a family of operators with a continuous trade-off between intrinsic and extrinsic features. Previous operators are either fully or partially intrinsic. In contrast, the proposed family spans the entire spectrum: from completely intrinsic (depending only on the metric) to completely extrinsic (depending only on the Gauss map). By adding an infinite potential well to this (or any) operator we can also robustly handle surface patches with irregular boundary. We explore use of these operators for a variety of shape analysis tasks, and study their performance relative to operators previously found in the geometry processing literature.

Downloads

BibTeX

@article{Liu:Dirac:2017,
  title = {A Dirac Operator for Extrinsic Shape Analysis},
  author = {Hsueh-Ti Derek Liu, Alec Jacobson, Keenan Crane},
  year = {2017},
  journal = {Computer Graphics Forum}, 
}

Patch Dataset

To enable further testing of methods for geometric texture classification, we have released our patch dataset.

Acknowledgements

Lucas Schuermann participated in an early version of this project. This work was funded in part by NSF Award 1319483 (under an REU supplement), NSERC Discovery Grants (RGPIN–2017–05235 & RGPAS–2017–507938), the Connaught Fund, a gift from Adobe Systems Inc., and a gift from Autodesk, Inc.