Next: 3.2.3 Charts
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.1 Constant Functions
Given the set 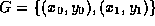 ,
consider the two functions
,
consider the two functions 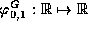 and
and
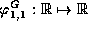 , defined as follows:
, defined as follows:
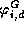 is a d-degree polynomial with
The above defines
is a d-degree polynomial with
The above defines 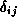 , the Kronecker delta.
The set G represents the function
, the Kronecker delta.
The set G represents the function 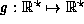 using two distinct elements of g:
we here envision the unary function g as a set, as defined in section
using two distinct elements of g:
we here envision the unary function g as a set, as defined in section  .
From this, we may deduce that G is also a function, and that
.
From this, we may deduce that G is also a function, and that 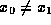 .
It follows that the functions
.
It follows that the functions 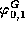 and
and 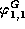 are well defined, for our choice of G.
Since
are well defined, for our choice of G.
Since 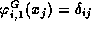 ,
the function
,
the function 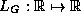 ,
interpolates G:
,
interpolates G:
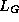 is the linear Lagrange interpolating polynomial of G.
is the linear Lagrange interpolating polynomial of G.
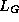 may be expressed in standard polynomial form:
may be expressed in standard polynomial form:
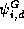 is the coefficient of
is the coefficient of 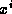 in
in 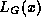 , a d-degree polynomial.
The leading coefficient,
, a d-degree polynomial.
The leading coefficient,
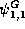 , is of special interest,
and may be denoted simply by
, is of special interest,
and may be denoted simply by 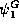 :
The set G, and the associated polynomial
:
The set G, and the associated polynomial 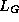 , are:
, are:
- monotonically decreasing if
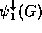 ,
, - constant if
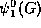 , and
, and - monotonically increasing if
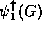 ;
;
where:
Consider 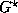 , a richer representation of g,
, a richer representation of g,
The representation 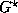 has one of the preceding
properties if all two-member subsets of
has one of the preceding
properties if all two-member subsets of 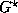 have the same property:
All three properties are considered to be satisfied by sparse representations of g since
where
have the same property:
All three properties are considered to be satisfied by sparse representations of g since
where 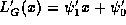 .
For G = g,
the usual definitions of constancy and monotonicity are equivalent
to those given here.
Let
.
For G = g,
the usual definitions of constancy and monotonicity are equivalent
to those given here.
Let 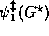 state that
state that 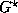 has one of the above properties:
For all representations
has one of the above properties:
For all representations 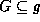 ,
,
The Lagrange interpolating polynomial 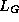 for
for 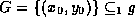 is defined as follows:
is defined as follows:
Using the constant and linear interpolating polynomials we will
construct constant bounds for many common functions.
Next: 3.2.3 Charts
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.1 Constant Functions
![]() ,
consider the two functions
,
consider the two functions ![]() and
and
![]() , defined as follows:
, defined as follows:
![]()
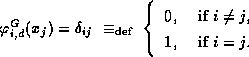
![]()
![]()
![]()
![]() may be expressed in standard polynomial form:
may be expressed in standard polynomial form:
![]()
![]()
![]()
![]() , a richer representation of g,
, a richer representation of g,
![]()
![]()
![]()
![]()
![]()
![]() for
for ![]() is defined as follows:
is defined as follows:
![]()