Next: 2.2 Rational Numbers
Up: 2 Numbers
Previous: 2 Numbers
The integer number system is a basic system of numbers.
The set of all integers is denoted by 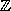 :
:
This number system is particularly simple and forms
the basis for all of the other number systems presented here.
Although the reader is assumed to be familiar with the integers,
some semi-formal discussion follows, which serves to refresh the reader's
memory and to illustrate common features of all number systems.
The integers can be constructed from the natural numbers;
purists construct the naturals using set theory [41, 17, 59].
Integers can be combined through addition and multiplication.
Operators abstract the notion of combining numbers, by allowing
for unary and 0-ary operators.
The terms function and operator are interchangable.
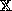 denotes a set of numbers.
An n-ary operator
denotes a set of numbers.
An n-ary operator 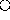 maps an n-tuple of numbers to a single number.
Formally stated,
maps an n-tuple of numbers to a single number.
Formally stated,
Addition and multiplication are binary operators.
An n-ary function 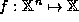 may
be represented as a set F, of n+1-tuples of numbers:
Boldface is used to indicate vectors.
may
be represented as a set F, of n+1-tuples of numbers:
Boldface is used to indicate vectors.
A set of numbers 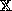 is closed under an n-ary operation
is closed under an n-ary operation 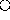 if
if
Integers are closed under addition and multiplication:
the sum or product of any two integers is another integer.
Since binary operators are so prevalent several properties
of binary operators will be relevant. A binary operator 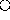 is commutative if
is commutative if
it is associative if
it has identity 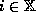 if
and it has
if
and it has 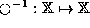 as an inverse if
where i is the identity for
as an inverse if
where i is the identity for 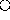 .
A unary operator g has an inverse
.
A unary operator g has an inverse 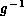 if
if
An n-ary function 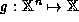 is total if
is total if
where 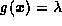 states that g
is undefined for agument
states that g
is undefined for agument  .
A function which is not total is a partial function.
The function g is injective (invertible) if
An inverse operator
.
A function which is not total is a partial function.
The function g is injective (invertible) if
An inverse operator 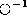 is a total inverse if it is a total operator,
otherwise it is a partial inverse. A set of numbers
is a total inverse if it is a total operator,
otherwise it is a partial inverse. A set of numbers 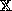 is closed under operator
is closed under operator 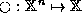 if and only if
if and only if 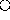 is total. The domain
of a function g is written formally as
is total. The domain
of a function g is written formally as 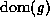 .
An n-ary function
.
An n-ary function 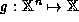 may be restricted to a set
may be restricted to a set 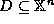 ,
so that
,
so that 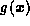 is not defined for
is not defined for 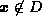 :
:
Negation is the total inverse of addition.
Subtraction is defined as the sum of a number with another
number's additive inverse:
A serious limitation of the integers is the lack of a
total inverse of multiplication. Division is
defined as the product of a number with another number's
multiplicative inverse:
It follows that the integers are not closed under division.
Addition and multiplication over the integers jointly satisfy
the following distributive law:
multiplication is said to distibute over addition.
Addition and multiplication over the integers do not satisfy
the following, alternative, distributive law:
The first distributive law will be hereafter referred to as
``the'' distributive law.
Another nice property of the integers is that comparing
any pair of integers will always result in exactly one of
three orderings. Equivalently, every pair of
distinct integers contains a larger member:
where 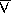 denotes exclusive or.
denotes exclusive or.
The comparison operator 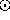 (
( 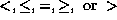 )
maps pairs of numbers to booleans:
)
maps pairs of numbers to booleans:
where 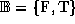 , the set of booleans.
, the set of booleans.
Common Practice
Almost all computers have hardware dedicated to performing
very quick operations on integers. Many systems strictly limit
the magnitude of the integers to guarantee certain
limits on computational resource requirements, while some do not.
Although the manipulations
of integers by computers is a fascinating and vitally important
research area we will envision integers as a basic data type
with rudimentary operations.
Next: 2.2 Rational Numbers
Up: 2 Numbers
Previous: 2 Numbers
![]() :
:
![]()
![]() denotes a set of numbers.
An n-ary operator
denotes a set of numbers.
An n-ary operator ![]() maps an n-tuple of numbers to a single number.
Formally stated,
maps an n-tuple of numbers to a single number.
Formally stated,
![]()
![]()
![]() is closed under an n-ary operation
is closed under an n-ary operation ![]() if
if
![]()
![]() is commutative if
is commutative if
![]()
![]()
![]()
![]()
![]()
![]() is total if
is total if
![]()
![]()
![]()
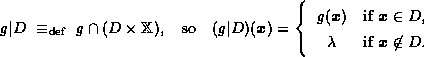
![]()
![]()
![]()
![]()
![]()
![]() (
( ![]() )
maps pairs of numbers to booleans:
)
maps pairs of numbers to booleans:
![]()