Next: 2.3 Real Numbers
Up: 2 Numbers
Previous: 2.1 Integers
The rational number system is an extension of the integer
number system [42]. The set of all rationals is denoted by
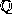 :
:
Each rational number is a ratio of two integers: a
numerator and a non-zero denominator.
The rationals
extend the integers since the integers are homomorphic to
the rationals. An injective mapping 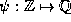 is a homomorphism if all the properties of
is a homomorphism if all the properties of  are preserved in
are preserved in 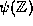 . The mapping
. The mapping
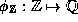 (abbreviated as
(abbreviated as 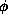 ),
is a homomorphism from
),
is a homomorphism from 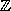 to
to 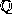 .
In order to verfiy this one must show
that:
and
When dealing with different
number systems in close mutual proximity it will be useful to
precisely specify operators as was done above.
With a formal definition of rational
addition and multiplication,
showing that
.
In order to verfiy this one must show
that:
and
When dealing with different
number systems in close mutual proximity it will be useful to
precisely specify operators as was done above.
With a formal definition of rational
addition and multiplication,
showing that 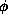 is a homomorphism is straightforward.
Because of the
simple homomorphism
is a homomorphism is straightforward.
Because of the
simple homomorphism 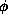 , the integers are commonly viewed as a
subset of the rationals.
, the integers are commonly viewed as a
subset of the rationals.
The nice properties of the integers
extend to the rationals. The rationals are closed
under addition and multiplication. Rational addition
has a total inverse as did integer addition.
Rational addition and multiplication are associative
and commutative; together they obey the distributive law.
Rational multiplication has an ``almost'' total inverse:
The inverse is not total because zero is not allowed in
the denominator of a rational. So the rationals are closed
under division, except for division by zero.
As with integers, comparisons between rational numbers
result in one of three orderings.
Most mathematicians do not view the lack of a total
multiplicative inverse as a major failing of the rationals.
Consider the squaring operator defined by:
The inverse of the squaring operator is the square root
operator, which satisfies the following:
There is no total square root operator over the rationals:
consider 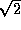 or
or 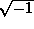 .
This is one reason to extend the rationals. Many popular
operators are not total over the rationals.
.
This is one reason to extend the rationals. Many popular
operators are not total over the rationals.
Common Practice
There are computer facilities, in the form of software libraries or hardware
assist, for performing operations
on rationals. These facilities store each rational as a pair
of integers [51], or as a continued fraction [36].
Although arithmetic operations (+, -,  , and
, and  )
can be performed with these libraries, many other
popular operations cannot be performed directly
since many popular operations are not total over the rationals.
It is also difficult to predict the computational resources
required for a string of operations since the time required
to perform an operation is dependent on the numbers involved.
Limiting the computational requirements usually results in a
system like floating point, which will be discussed shortly.
)
can be performed with these libraries, many other
popular operations cannot be performed directly
since many popular operations are not total over the rationals.
It is also difficult to predict the computational resources
required for a string of operations since the time required
to perform an operation is dependent on the numbers involved.
Limiting the computational requirements usually results in a
system like floating point, which will be discussed shortly.
Next: 2.3 Real Numbers
Up: 2 Numbers
Previous: 2.1 Integers
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , and
, and ![]() )
can be performed with these libraries, many other
popular operations cannot be performed directly
since many popular operations are not total over the rationals.
It is also difficult to predict the computational resources
required for a string of operations since the time required
to perform an operation is dependent on the numbers involved.
Limiting the computational requirements usually results in a
system like floating point, which will be discussed shortly.
)
can be performed with these libraries, many other
popular operations cannot be performed directly
since many popular operations are not total over the rationals.
It is also difficult to predict the computational resources
required for a string of operations since the time required
to perform an operation is dependent on the numbers involved.
Limiting the computational requirements usually results in a
system like floating point, which will be discussed shortly.