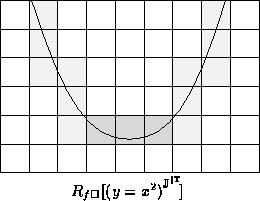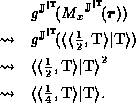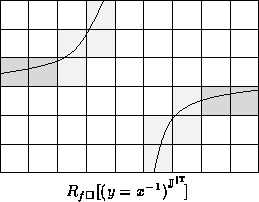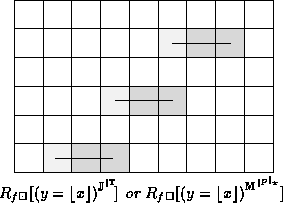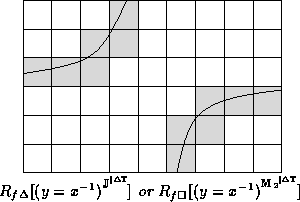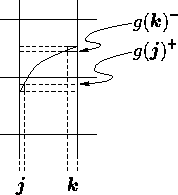
Next: 4.3.1 Optimization: Super-Pixel Rendering
Up: 4 Graphs
Previous: 4.2.8 Sequential Rendering
Rather than building up the rendering pixel by pixel,
the rendering may be built up row by row, or column by column.
Each row, or column, is visited once.
Consider rendering y = g(x), where 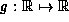 .
An example rendering follows:
.
An example rendering follows:
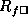 denotes a rendering produced using
column, or row, testing.
The function g is evaluated for each column.
An example evaluation follows:
After
denotes a rendering produced using
column, or row, testing.
The function g is evaluated for each column.
An example evaluation follows:
After 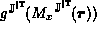 is evaluated,
pixels of R may be appropriately set.
If
is evaluated,
pixels of R may be appropriately set.
If 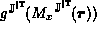 spans a
single pixel, that pixel may be set to
spans a
single pixel, that pixel may be set to 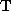 ;
pixels untouched by
;
pixels untouched by 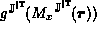 may be set to
may be set to 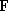 .
.
Another example rendering follows:
Finer tests may be performed, as with pixel-based testing.
Using sample testing, g is evaluated for a portion of each
partially undetermined column.
An example rendering follows:
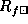 denotes a rendering produced using sub-column, or sub-row,
sample testing.
The portions chosen for the above rendering lay on the left
side of each pixel column. Another pass, choosing portions
on the right side of each pixel column, would set
the remaining undetermined pixels to
denotes a rendering produced using sub-column, or sub-row,
sample testing.
The portions chosen for the above rendering lay on the left
side of each pixel column. Another pass, choosing portions
on the right side of each pixel column, would set
the remaining undetermined pixels to 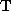 .
.
An example rendering, produced using sub-column
continuity-based testing, follows:
Continuity-based testing allows column based
testing to set long columns of pixels to
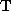 with a single test.
With continuity-based testing,
with a single test.
With continuity-based testing, 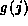 and
and
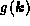 are computed; if g is continuous over
are computed; if g is continuous over
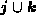 then g is known to smoothly pass
from
then g is known to smoothly pass
from 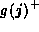 to
to 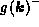 if
if 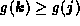 ;
g is known to smoothly pass
from
;
g is known to smoothly pass
from 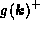 to
to 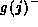 if
if 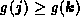 .
The following diagram illustrates a portion of a single column from the
preceding rendering:
Similar results may be obtained with
linear interval arithmetic, without bothering
with continuity-based testing. Continuity information
is still quite important, however.
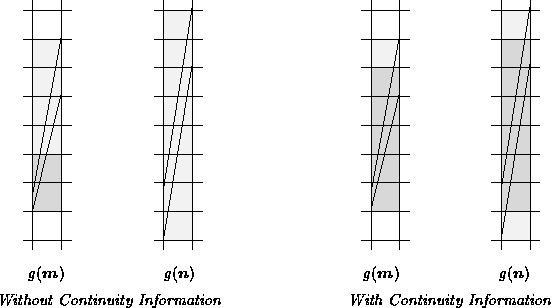
The following diagram illustrates the information
gained by a linear interval arithmetic evaluation
of g, with and without continuity information:
Without
continuity information,
pixels that completely enclose
.
The following diagram illustrates a portion of a single column from the
preceding rendering:
Similar results may be obtained with
linear interval arithmetic, without bothering
with continuity-based testing. Continuity information
is still quite important, however.
The following diagram illustrates the information
gained by a linear interval arithmetic evaluation
of g, with and without continuity information:
Without
continuity information,
pixels that completely enclose 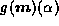 , for any
, for any  ,
may be set to
,
may be set to 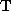 ; determining such pixels is straight-forward.
Such determination mimics the rules behind determining
; determining such pixels is straight-forward.
Such determination mimics the rules behind determining
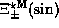 ; see section
; see section  .
With continuity information, g must smoothly
pass from
.
With continuity information, g must smoothly
pass from 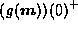 to
to 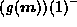 if
if 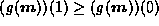 ;
g must smoothly pass from
;
g must smoothly pass from 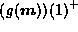 to
to 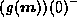 if
if 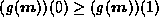 .
.
Of course, row and column testing may be used on specifications
containing inequalities. Logical combinations of equations
and relations are easily accommodated, by passing row
or column descriptions along with evaluation results
when evaluating the upper levels of S.
Next: 4.3.1 Optimization: Super-Pixel Rendering
Up: 4 Graphs
Previous: 4.2.8 Sequential Rendering
![]() .
An example rendering follows:
.
An example rendering follows: