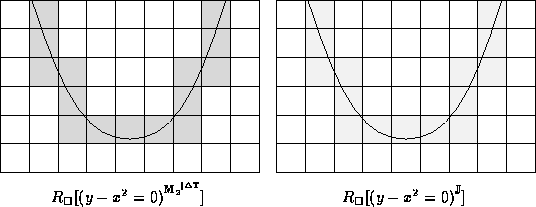
As before, a rendering is built pixel by pixel. The four tests described in the previous section may be utilized with linear interval arithmetics. The tests simply utilize linear interval arithmetic in place of constant interval arithmetic.
For line-like renderings, subpixel testing is not always required when using a linear interval arithmetic. Consider the following two renderings:

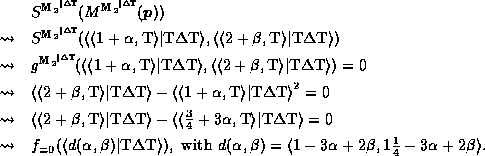
![]()
![]()
![]()
Of course, subpixel evaluation is still needed to combat the interval over-estimation usually present in large specifications. Continuity information is usually needed when rendering specifications involving equality.
The following two renderings were produced using constant interval arithmetic and all of the subpixel tests described:
![]()
![]()
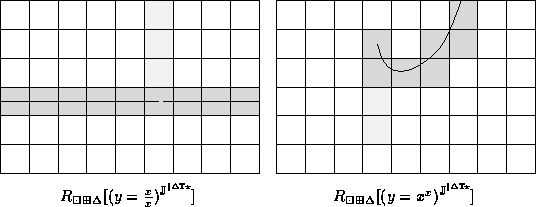
The light grey pixels may be resolved with linear interval arithmetic since operations may consider the dependence of the interval arguments upon the system parameters, namely x and y. For our preceding examples, note that
![]()
![]()
The following two renderings were rendered using linear interval arithmetic:
| Jeff Tupper | March 1996 |