VectorAdam for Rotation Equivariant Geometry Optimization NeurIPS 2022

On the left, we optimize the ARAP energy for a triangle mesh with 200 vertices for 100 iterations with 1000 randomly rotated initial configurations. (a) shows the gradients at first optimization step from Adam and VectorAdam. (b) shows the histograms of the angular distribution of these 20M gradient directions. Gradient Descent and VectorAdam exhibit their rotation equivariance by presenting a uniform distribution, while Adam presents a biased distribution with spikes at 45◦ angles. On the right in (c), we observe similar coordinate-system bias on a input point cloud, when adverserially optimize inputs to a 3D classifier

Abstract

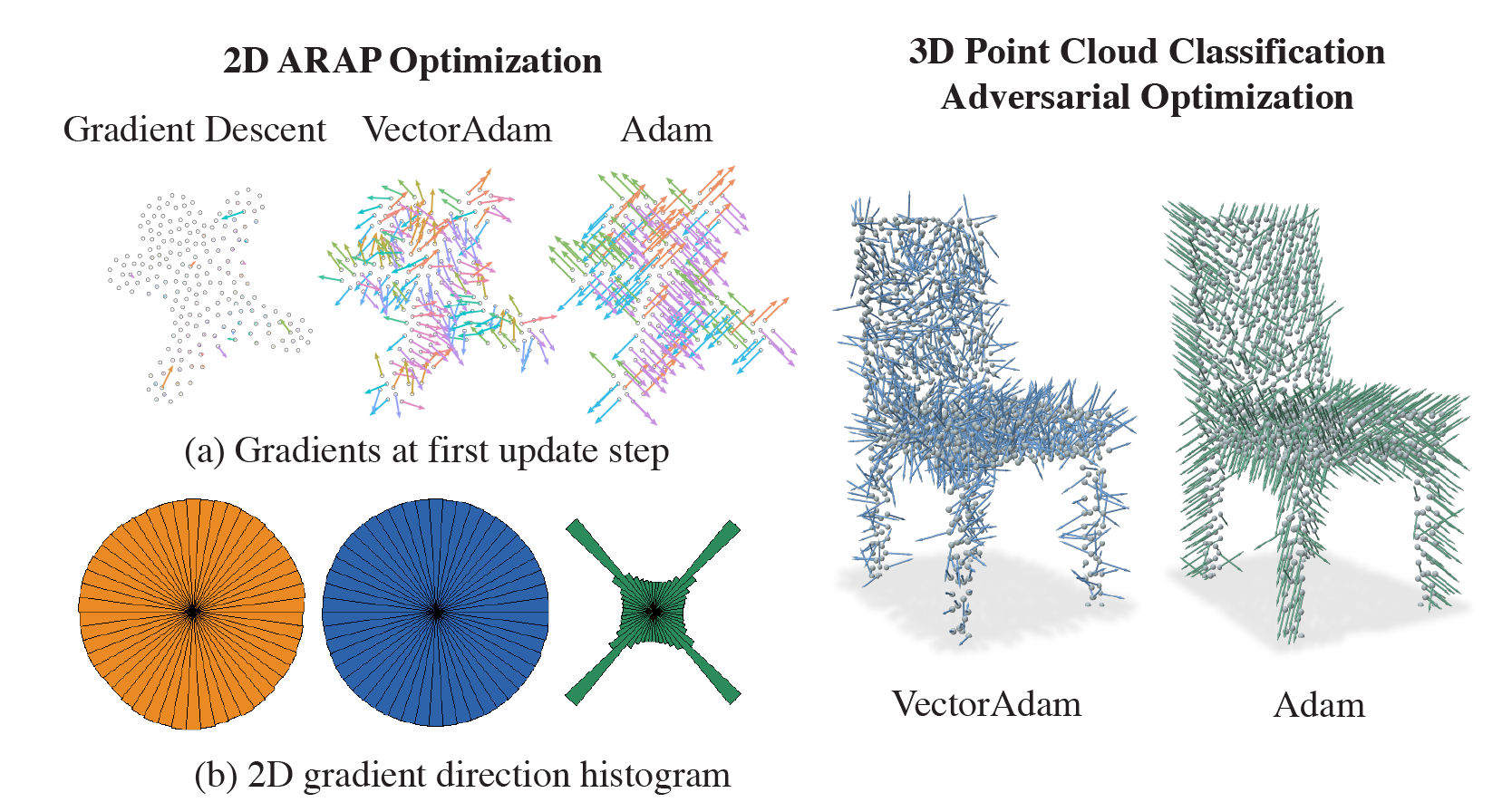
The Adam optimization algorithm has proven remarkably effective for optimization problems across machine learning and even traditional tasks in geometry processing. At the same time, the development of equivariant methods, which preserve their output under the action of rotation or some other transformation, has proven to be important for geometry problems across these domains. In this work, we observe that Adam — when treated as a function that maps initial conditions to optimized results — is not rotation equivariant for vector-valued parameters due to per-coordinate moment updates. This leads to significant artifacts and biases in practice. We propose to resolve this deficiency with VectorAdam, a simple modification which makes Adam rotation-equivariant by accounting for the vector structure of optimization variables. We demonstrate this approach on problems in machine learning and traditional geometric optimization, showing that equivariant VectorAdam resolves the artifacts and biases of traditional Adam when applied to vector-valued data, with equivalent or even improved rates of convergence.

Downloads

• Paper
• Arxiv
• Code

Supplemental Video

BibTeX

@article{ling2022vectoradam,
    title={VectorAdam for Rotation Equivariant Geometry Optimization},
    author={Ling, Selena and Sharp, Nicholas and Jacobson, Alec},
    journal={arXiv preprint arXiv:2205.13599},
    year={2022}
  }

Acknowledgements

Our research is funded in part by the New Frontiers of Research Fund (NFRFE–201), the Ontario Early Research Award program, the Canada Research Chairs Program, a Sloan Research Fellowship, the DSI Catalyst Grant program, Fields Institute for Mathematical Sciences, the Vector Institute for AI, gifts by Adobe Systems. We also thank Wenzheng Chen for helpful discussions, John Hancock for technical support, and the anonymous reviewers for their helpful comments.