The viewing direction is set to be normal to the face being recorded. The terrain is then rendered normally, and the required image then occupies the entire window. This image is then read directly from the frame buffer, and stored in an array to be used later as a texture. In addition to the image, the contents of the depth buffer, and the camera matrix (to be discussed in the warping section) need to be stored as well. Only with all three of these pieces of information can accurate warping be done.
This process is done for all visible faces from all sample points, completing the pre-computation phase. If these images are used without warping, then the terrain looks correct only when the current interactive viewpoint lies exactly on one of the sample points. As one moves away from this point, the terrain looks as though it's stretching or shrinking on the imposter faces, which is expected since there is no depth to the images. To achieve accurate movement, one must warp the images using depth information.
The following images were all taken from an viewpoint which lies exactly on one of the sampling points. In this case texture mapping without warping is totally accurate (as is image warping, since the warping transformation becomes the identity on the sample points).
 |
 |
 |
| Fig. 1: Terrain rendered normally | Fig. 2: Texture mapped imposter, no warping | Fig. 3: Texture mapped imposter with warping |
3.0 Warping Images
Image warping can be done in two general ways. Once the image to warp
has been selected (I1), one can go through each pixel of the image and
determine its position in the new image (I2). This forward-mapping method
results in holes in the warped image, because many pixels in I2 do
not get filled in by the mapping.
The alternative is to go through the pixels in I2 and map each one
back to a pixel in I1, filling in the new pixel with the resultant
colour. This backward-mapping method eliminates the hole problem, but
requires that the depth of each pixel in I2 be known before warping
begins. Therefore the depths of I1 must be forward mapped first. This
whole process is now discussed in further detail.
3.1 Selecting an image I1
Each time the current viewpoint is moved, the horizontal and vertical
angles between the current point and the center of the sampling
hemisphere are recalculated. The closest sample point is then found
simply by choosing one which has the smallest difference in both the
horizontal vertical angles. The image(s) recorded at this point are
then used to generate the warped images for the current viewpoint.
3.2 Forward mapping the depths
This section discusses the transformation from I1 to I2. It was
mentioned previously that when sample images are recorded, the camera
matrix used to generate each image is recorded as well. The camera
matrix maps points from world coordinates (WCS) into normalized device
coordinates (NDCS). Therefore, in terms of openGL, the camera matrix
is defined as the projection matrix (PJ) times the modelview matrix
(MV): [CAM1] = [PJ][MV]. (Note: matrices in openGL are stored in
column-major form).
The transformation requires that a camera matrix for the current viewpoint must also be calcluated. Therefore the view frustum must be set up as described in the previous section from the current eye position, and the view direction must be set as described (with gluLookAt). Once this is done, the projection and modelview matrices are extracted from the matrix stack, and multiplied to form the new camera matrix CAM2.
In order to map points from I1 to I2, each pixel must be mapped from NDCS back into WCS, and then from WCS into NDCS of CAM2. Therefore the full transformation matrix is computed with:
[T12] = [CAM2][invCAM1]
This maps points (x1, y1, z1, 1) to (w2x2, w2y2, w2z2, w2). The w2 term is then divided out to get (x2, y2, z2, 1) in NDCS.
Using T12, the depth (or z value) of each pixel in I1 can be forward mapped into I2. Note that T12 transforms from NDCS to NDCS; all point lie in a cube from (-1, -1, -1) to (1, 1, 1). A viewport transformation must be done on both ends to complete the transformation to the device coordinate system (DCS). This simply a matter of transforming points in the range (-1,-1) - (1,1), to (0,0) - (xMax, yMax), or vice versa (the z value is no longer needed).
As previously discussed, forward-mapping results in holes in the
warped image. The forward-mapped depths will have this problem, so
before backward-mapping the image, the holes must be filled. This
problem will be discussed in a later section.
3.3 Backward-mapping the image
Backward mapping involves taking points from I2 and transforming them
to a point in I1. The transformation is given by:
[T21] = [CAM1][invCAM2]
This transforms points (x2, y2, d2, 1) in NDCS to points (w1x1, w1y1, w1d1, w1) in CCS. Dividing out the w1 term completes the transformation into NDCS. Using this matrix, we can fill in the luminosity at (px2, py2) on I2 with the values found at (px1, py1) on I1, where px1 is a value in DCS (after the viewport transformation). This transformation is done only with points on I2 which had a depth set by forward mapping the depths of I1, or by the hole-filling procedure. Some results are seen below.
 |
 |
 |
| Fig. 4: Terrain rendered normally | Fig. 5: Texture mapped imposter, no warping | Fig. 6: Texture mapped imposter with warping |
One can see in figure 5 that using texture mapping without warping results in a distorted image when the viewpoint does not sit on one of the sample points. Figure 6 uses warping, which results in a more accurate image. However, there are terrain sections visible from the current viewpoint which were not visible from the nearest sample point. This results in the missing sections in the warped image.
 |
 |
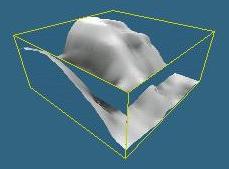 |
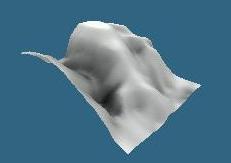
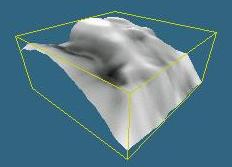
| Fig. 7: Terrain rendered normally | Fig. 8: Texture mapped imposter, no warping | Fig. 9: Texture mapped imposter with warping |
These figures illustrate another problem with image warping. Although figure 9 has a more accurate outline than figure 8, pieces are missing at the edges of the faces. This is again a result of moving away from the sample point; sections of terrain which now should be seen on one particular face were not seen through that face from the sample point, so the image being warped does not contain all of the necessary information.
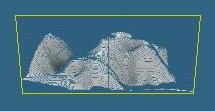
4.0 Hole-filling
As discussed in section 3.0, a forward mapping transformation leaves holes in the resultant image. This is the case with depth map, and the holes need to be filled for the image warping results to look reasonable. Two methods of hole filling were used.
8 neighbor average
This algorithm scans through each pixel in the depth image of I2. If the pixel has no depth yet, all eight neighbouring pixels are examined, and the depth of each, if it exists, is recorded. If 5 or more of the neighbouring pixels have a depth, then the current pixel is set to the average of those. Otherwise nothing is done.This algorithm fills in smalls holes with single pixel width, but leaves larger ones untouched.
Using the image outline
This algorithm first attempts to determine the outline of the image, by scanning in from each side of the image until a pixel with a depth is found. All pixels scanned before a pixel with depth is found (along the current scanline) is said to be outside of the image. After this process, the border of the image is completely defined. Now the 8 neighbour algorithm is run again, this time only on unfilled pixels within the image. These pixels can be filled regardless of the number of neighbours which have a depth. Therefore the larger holes can be filled.The results of both algorithms can be seen below.
 |
 |
 |
| Fig. 10: No hole filling | Fig. 11: With 8 neighbour algorithm | Fig. 12: With 8 neighbour and outline |
5.0 Recording extra information for edge
continuity
In the previous pre-recording process, only the exact image to be put
on the imposter face was recorded. This was done originally so that
when one uses texture mapping without warping, the image looks as
accurate as possible. However, with warping, it becomes useful to
record more information, by expanding the width and height of the face
being recorded. With more of the terrain information recorded on each face, one
can move further away from the sample point without seeing gaps at the
edges of the imposter faces.
 |
 |
 |
| Fig. 13: Terrain rendered normally | Fig. 14: Texture mapping, no warping or border | Fig. 15: Warping with no border |
 |
||
| Fig. 16: Warping with 1/5 border |
Figure 16 shows results when the size of the recorded face is increased by 1/5 of the width of the original face; the gap is completely filled in. However, expanding the border too much causes a new problem: hole-filling becomes more difficult, which can cause artifacts seen in section 4. This is because a larger space is being recorded onto an image whose size does not change. Therefore the terrain on the pre-recorded image becomes smaller. This results in more and larger holes in the forward mapping of the depth (since we are mapping from a small terrain image to a larger one). It was found that expanding the border more than 1/5 results in more holes than the hole-filling procedures could handle correctly.
6.0 Timing Results
The following tables give the timing results for rendering the terrain
in various modes. The time measurements were all taken when only the
front face of the imposter was visible, as in figures 4 - 6. The
results for more than one face are not shown, but can be approximated
by multiplying these results by the number of visible faces. Of course
when rendering without imposters, it does not make a significant
difference where the viewpoint is.
These timings are somewhat variable as the viewpoint moves, but do not tend to deviate more than indicated. Note that the breakdown of using imposters with warping does not add up to the total rendering time. The majority of the extra time is used in creating a texture map from the warped image, and drawing it on the appropriate face.
Total rendering time (seconds +- 0.02)
| Normal rendering | 0.05 |
| Texture mapped imposter, without warping | 0.13 | Imposter with warping | 0.45 |
Breakdown of image warping time (seconds +- 0.01)
| Forward mapping the depths | 0.13 |
| Hole filling | 0.08 |
| Backward mapping the image | 0.11 |
The program was run on a dual Pentium II 333Mhz processor, with a software openGL implementation.
7.0 Conclusions
Cleary with this terrain model, using imposters significantly
slows down the rendering time, and therefore is not
practical to use. Even
using simple texture mapping without warping is noticeably slower
than normal rendering (although the texture mapping alone could be
sped up with use of texture objects). However, all of the time taken
in rendering an imposter is dependent only on the window size, not the
scene complexity. The warping and hole-filling steps are exactly the
same for a scene of any complexity. Further complexity (this scene
contains 4608 triangles) would increase the normal
rendering time, but the imposter times would stay
constant. Only the pre-processing time would increase.