Part 1 -- programming portion [10 points]

This portion of the assignment must be submitted electronically with "make submit", by Saturday morning Feb 16 just before 5 am.

Objective: implement a class to store compressed images using a quadtree representation.

The code:

   Makefile
   global.h - contains definition of ASSERT() macro
   QuadTree.h - you'll probably want to modify this
   QuadTree.cpp - you must complete the code in here
   testQuadTree.cpp - wrapper program
   input1.txt - sample test case
   output1.txt - sample test case

   template - new template file

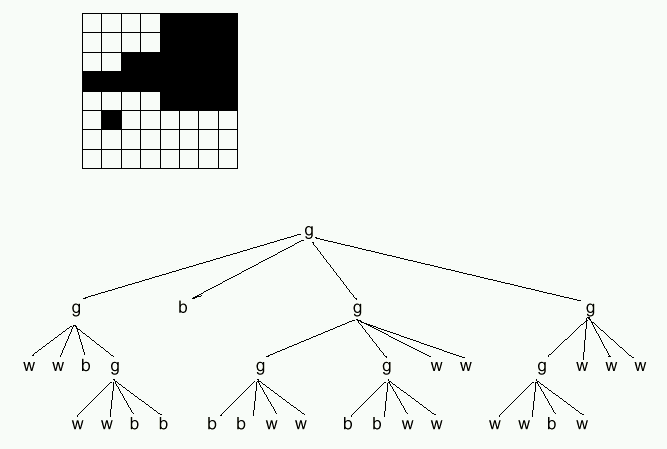
About quadtrees: A quadtree is a hierarchical data structure usually used to store information about an image or a 2D space. In a quadtree, space is recursively subdivided into quadrants.

We will use quadtrees to store 2D square monochrome images whose dimensions are a power of 2. Below is an example of a bitmap image and the corresponding quadtree. The root node corresponds to the entire image, and each of its children corresponds to one quarter of the image. Nodes are labelled b, w, or g, for black, white or grey. If all the pixels covered by a node are the same colour (black or white), there is no need to have children under the node. This allows us to compress images, especially when the image contains many large homogeneous regions. Grey nodes are ones that do not cover uniformly coloured pixels, and therefore have 4 children.

Your implementation: You must use a quadtree representation to store the image internally. Furthermore, your tree must be composed of the minimum number of nodes necessary to store the image. Part of the autotesting procedure will check if getNumNodes() returns the correct number for various different images.

You may change QuadTree.h (for example, adding private methods or data members), but if you change the public interface already provided in QuadTree.h you will likely fail all autotests.

Note that, although the computeUnion() and computeIntersection() methods may look daunting, there is at least one simple and elegant way to implement them (it involves adding at least one other method to the class). Try to think creatively before sitting down to implement these methods.

Note that the QuadTree::computeIntersection() method is optional and need not be implemented (see next paragraph).

Marking scheme and bonus: 5 marks will be awarded if your code passes all autotesting. The other 5 marks will be based on your coding style. The QuadTree::computeIntersection() method is optional and will earn you 1 bonus mark if you implement it correctly.

Style marks:

• You are required to make methods inline whenever it is appropriate. This will involve modifying QuadTree.h.
• Do not write any lines of code that exceed 80 characters. If any of your lines exceed 80 characters, break them up into smaller lines.
• Make sure there are no memory leaks in your code. Use delete or delete [ ] appropriately.
• Try to refactor code wherever you can. If two parts of your program do very similar things, try to pull out the common part between them and put it in a subroutine (i.e. another (private) method, or a function).
• If you define any new methods in your class, make them public or private appropriately, and use the const keyword appropriately.

Compiling, running, testing, submitting: The Makefile contains appropriate targets so that you can do "make", "make run", "make test", and "make submit" just as you did in the last assignment. Do NOT use submitcsc191s to submit; you must use "make submit". If you encounter problems submitting, go to the supervised lab hours for help; or, go to the course homepage, read the announcement made Jan 30, and follow the instructions. Late assignments will not be accepted. If you absolutely cannot get "make submit" to work, email me your source code BEFORE the assignment deadline.

Remember that you must be on skule.ecf for submission to work. If you run "hostname" and it doesn't say "skule.ecf", then you're not on skule.ecf. You must ssh or otherwise connect with skule.ecf.

As can be seen by inspection of the Makefile, the only source files that will be submitted are QuadTree.h and QuadTree.cpp. In addition, you will need a copy of the template file in your working directory. DO NOT use the old template file under /share/copy/csc191s/ that was used in assignment 1. Instead, get the new template file (see link above) and fill in your name, ID number, and assignment number.

Part 2 -- a mathematical exercise [5 points]

Below are 4 steps in approximating the snowflake curve. The first approximation (n=1) is an equilateral triangle. As discussed in lecture, each successive approximation is generated by replacing the middle third of each edge with two new edges meeting at a 60 degree angle.

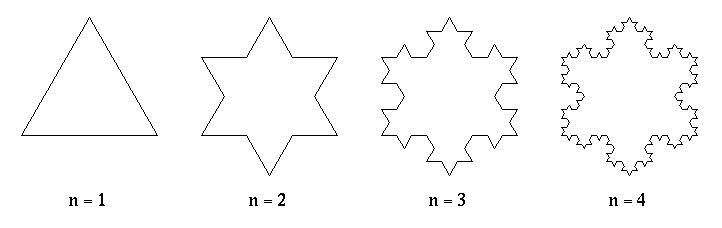
a)
Let P(n) and A(n) be the perimeter and area, respectively, of each approximation of the snowflake curve, as functions of n, where P(1) = 3 and therefore A(1) = (3^0.5)/4. (Note that 3^0.5 is the plain ASCII text way of writing "3 raised to the exponent 0.5", or in other words the square root of 3.) You must derive exact, closed form expressions for P(n) and A(n). (Note that closed form expressions cannot contain infinite summations, and must not be defined recursively.) Show how you derived your expressions. To help you, you may find it useful to refer to some of the summation identities given in Shaffer on page 31 (equations 2.1 through 2.6).

b)
Evaluate the limits of P(n) and A(n) as n goes to infinity. What conclusion can you draw ?

c)
Make sure the sheet(s) of paper you hand in is identified at the top with your full name, student id number, email address, and is titled as "CSC 191 Assignment 2".

Marking scheme: 2 marks for part a), 2 marks for part b), and 1 mark for orderly and logical presentation.