2.15.5 Converging Intervals

A real number r is represented by a converging sequence of rational intervals:

This representation is well suited to algorithmic manipulation. All common operations are well defined using interval arithmetic, as will be demonstrated in the next chapter.

A basic number, such as , is provided as a computer program which produces consecutive terms of a representation of that basic number. Each term of the infinite sequence is produced after a finite number of operations is performed. Numbers can be combined by using interval arithmetic on the produced streams. It can be shown that the resulting stream also converges:

This assumes that the expression defines a real number. Some expressions, such as 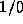, do not define a real number. Using 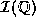will cause delays to be introduced into the system. For example, a division will not produce output until the denominator does not contain zero. After this initial delay of d terms, one term is output for each set of input terms provided (one input term for each input stream). A system with this input-output relationship is termed an on-line arithmetic system. No delay will occur using 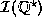, although the produced stream may begin with 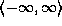terms.

The value of any finite expression, built with the provided operators and basic numbers, can be determined to any reasonable accuracy:

The function 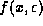is computable, as it simply computes successive terms of the representation of x until 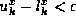, and then returns k. This contrasts strongly with the previous representations. No algorithm, using a finite number of computable atomic operations, can compute:

• the first digit of a decimal expansion of r,
• the first term of a continued fraction representation of r,

as discussed in the literature [62, 42, 12]. Note that 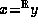does not imply 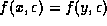, where x and y are two different real number representations. The remaining representations are special forms of the general converging interval representation of real numbers.

Jeff Tupper

March 1996