Next: 2.9.7 Functional Intervals
Up: 2.9 Generalized Interval Arithmetic
Previous: 2.9.5 Quadratic Intervals
A number may describe something with several parameters.
Several parameters may be integrated into the number system.
The simplest such system is 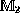 , where
the interval bounds are linear functions of
, where
the interval bounds are linear functions of  and
and 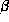 :
:
Each parameter  and
and 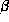 may independently
vary from zero to one.
may independently
vary from zero to one.
In general, 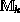 is defined as a real
linear interval number system with k parameters.
Each parameter may vary from zero to one independently:
is defined as a real
linear interval number system with k parameters.
Each parameter may vary from zero to one independently:
The term linear interval was chosen over affine interval
due to familiarity. Although the bounds are techincally
affine functions, an interval system which used linear functions
would not see much use. As will be seen when interval
arithmetic application algorithms are discussed, there will often
be a mapping from an ``actual'' parameter 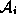 to a system
parameter
to a system
parameter 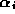 to allow for more complex parameter domains.
Forcing the upper and lower bounds to be zero when
to allow for more complex parameter domains.
Forcing the upper and lower bounds to be zero when 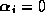 would severely restrict these mappings, and the applicability
of interval methods.
would severely restrict these mappings, and the applicability
of interval methods.
Consider our example problem,
of determining the range of a function over a given domain.
The linear interval chosen to represent the domain [a,b]
was 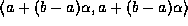 . The upper and lower
bounds are not always linear functions,
since
. The upper and lower
bounds are not always linear functions,
since 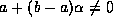 for
for 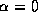 .
.
Next: 2.9.7 Functional Intervals
Up: 2.9 Generalized Interval Arithmetic
Previous: 2.9.5 Quadratic Intervals
![]() , where
the interval bounds are linear functions of
, where
the interval bounds are linear functions of ![]() and
and ![]() :
:
![]()
![]() is defined as a real
linear interval number system with k parameters.
Each parameter may vary from zero to one independently:
is defined as a real
linear interval number system with k parameters.
Each parameter may vary from zero to one independently:
![]()
![]() . The upper and lower
bounds are not always linear functions,
since
. The upper and lower
bounds are not always linear functions,
since ![]() for
for ![]() .
.