![]()
The approach taken for binary functions with constant interval arithmetic may be used with linear interval arithmetic. As before, we focus on binary grid functions. When presented with a binary function, we will cut it into sections where each section may be extended to a grid function which fits into a class.
As with unary functions, we will partition the domain based on monotonicity, so we may handle the upper and lower bounds independently. Concavity is also used when partitioning:
![]()
![]()
An upper bound will be determined for ![]() in two stages: first, a bilinear upper bound
in two stages: first, a bilinear upper bound ![]() of
of ![]() will be determined; then, a linear upper bound of h will be constructed;
this upper bound will be an upper bound of g.
A function
will be determined; then, a linear upper bound of h will be constructed;
this upper bound will be an upper bound of g.
A function ![]() is bilinear if
both
is bilinear if
both ![]() and
and ![]() are linear.
are linear.
An approximate upper bound ![]() is constructed from g:
is constructed from g:
![]()
![]()
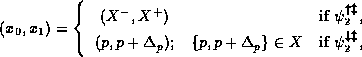
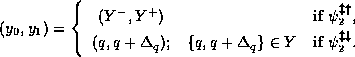
![]()
![]()
When ![]() ,
, ![]() is an upper bound.
This is shown by the following proof by contradiction;
the diagram given accompanies the proof.
is an upper bound.
This is shown by the following proof by contradiction;
the diagram given accompanies the proof.
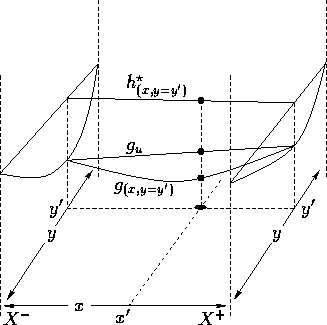
![]()
When ![]() ,
,
![]() is again an upper bound,
and may be proven with a similar argument, which follows.
is again an upper bound,
and may be proven with a similar argument, which follows.
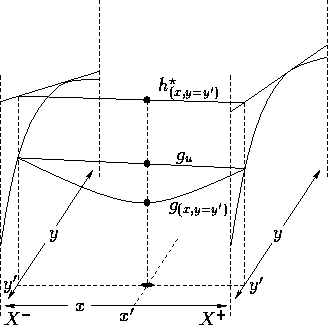
![]()
When ![]() ,
,
![]() is again an upper bound,
and may be proven with the preceding argument.
Alternatively, one may consider g'(x,y) = g(y,x),
after ensuring that
is again an upper bound,
and may be proven with the preceding argument.
Alternatively, one may consider g'(x,y) = g(y,x),
after ensuring that ![]() .
.
The proof does not hold for the last case,
when ![]() .
In any of the other three cases,
we may take
.
In any of the other three cases,
we may take ![]() ;
in this last case, we must further
test g to determine an upper bound.
We will not dwell on this since another
method will be presented shortly.
;
in this last case, we must further
test g to determine an upper bound.
We will not dwell on this since another
method will be presented shortly.
After h is determined, we construct a linear upper bound
of ![]() from
from
![]() .
Given that
.
Given that
![]()
| Jeff Tupper | March 1996 |