[ CLR 13 ]
The height of a BST is number of nodes on the longest
root-to-leaf path.
Some definitions of height will use the number of edges, instead.
It doesn't really matter when doing asymptotic analysis, since the
number of nodes and the number of edges differ by only one.
Insert, Delete, and Search take worst-case
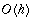 in a BST of
height h.
in a BST of
height h.
A BST of n nodes is balanced if height is in
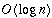 .
A balanced tree supports efficient operations, since most operations
only have to traverse one or two root-to-leaf paths.
.
A balanced tree supports efficient operations, since most operations
only have to traverse one or two root-to-leaf paths.
There are many implementations of balanced BSTs, including AVL
trees, 2/3 trees, and Red-Black trees. We'll discuss Red-Black trees.
[ CLR 14 ]
Every node in a Red-Black tree stores data (which includes the
key), a left child pointer, a right child pointer, a parent pointer,
and a ``colour'' attribute. A Red-Black tree satisfies the following
properties:
- Every node is either red or black.
- If a node has a NULL child, that "child" is considered black.
- If a node is red, then both of its children are black.
- Every simple path from a node to a descendant NULL child has the same number
of black nodes, (including the black NULL child).
- The root is black.
Here's an example of a Red-Black tree, where the square black nodes
are the ``virtual'' black children of Property II.
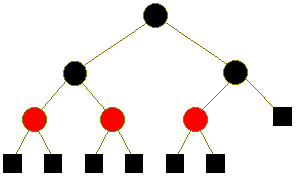
These five properties ensure that a Red-Black tree is balanced.
Intuitively: Property IV ensures that a Red-Black tree is balanced
if it doesn't contain red nodes, since every root-leaf path has the
same number of black nodes. When red nodes are added, Property III
ensures that, on a root-to-leaf path with k black nodes, there are at
most k red nodes. So adding the red nodes only increases the height
by a factor of two.
Let BH(x) be the number of black nodes on every x-to-leaf path. By
Property IV, each such path has the same number of black nodes.
For example: 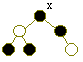 BH(x) = 2
BH(x) = 2
Lemma
A subtree rooted at x has at least
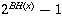 nodes.
nodes.
Intuition
Suppose x's subtree has only black nodes. By Property IV the tree
is complete,
For example: 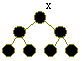 BH(x) = 3, number of nodes = 7
BH(x) = 3, number of nodes = 7
and it has
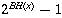 nodes. If red nodes are included, BH(x)
doesn't change, so number of nodes is still at least
nodes. If red nodes are included, BH(x)
doesn't change, so number of nodes is still at least
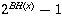 .
.
Lemma
Let h be the height of the tree. Then
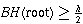 .
.
Intuition
By Property III, each root-to-leaf path has at least
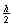 black nodes. (Otherwise, two red nodes would appear together, as
parent and child.) Thus,
black nodes. (Otherwise, two red nodes would appear together, as
parent and child.) Thus,
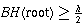 .
.
Theorem
The height, h, of a Red-Black tree is in
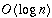 .
.
Proof
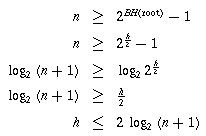
Since
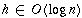 , a Red-Black tree is balanced.
, a Red-Black tree is balanced.