Suppose that we already implemented the Merge procedure (below,
we'll discuss the implementation). Merge can be used to make very
simple Insert and DeleteMin procedures:
The Merge procedure takes two leftist trees, A and B, and returns a
leftist tree that contains the union of the elements of A and B. In
a program, a leftist tree is represented by a pointer to its root.
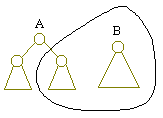
In merging, the simplest case occurs when one tree is empty (i.e. the pointer
to the root is NULL). In this case, just return the other.
Otherwise, what is the root of the merged tree?
It's A's root if A has the smaller key; it's B's root if B has the smaller key.
Suppose A's root has the smaller key. (If this isn't the case,
simply swap the A and B pointers.) Then we can merge right(A) with B:
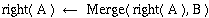
Now right(A) has changed. Its dist() may have grown larger in the
process, violating the second property above. If so, just swap
right(A) and left(A):
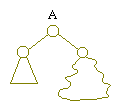 if dist(right(A)) > dist(left(A)), swap right(A) and left(A).
if dist(right(A)) > dist(left(A)), swap right(A) and left(A).
Finally, since dist(right(A)) might have changed, we have to update dist(A):
dist(A)
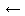 1 + dist(right(A))
1 + dist(right(A))
Of course, if right(A) = NULL, we'll assume that dist(right(A)) = -1.
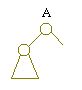 dist(right(A)) = -1
dist(right(A)) = -1
So the whole Merge procedure looks like this:

Note: If a node's child is NULL, that child's dist is assumed to be -1.
This isn't always checked in the code above!
Since each recursive call goes down either A's right path,
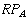 ,
or B's right path,
,
or B's right path,
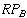 , the number of calls is at most the
sum of the lengths of the right paths:
, the number of calls is at most the
sum of the lengths of the right paths:
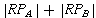 and
and
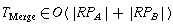
since other operations in the body of Merge are
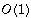 . In other words,
. In other words,
 ,
,
since
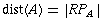 . But what is
. But what is
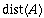 in a
tree of
in a
tree of
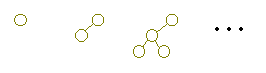
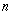 nodes? Let's look at some examples:
nodes? Let's look at some examples:
if dist(A) = 0,
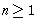 .
. |
 |
if dist(A) = 1,
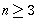 .
. |
 |
if dist(A) = 2,
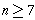 .
. |
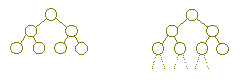 |
So the pattern is:
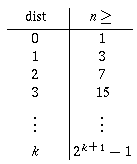
So if
 . This makes
sense, since the tree must be full down to the dist(A) level
(otherwise, the second property would be violated!).
. This makes
sense, since the tree must be full down to the dist(A) level
(otherwise, the second property would be violated!).
A full tree of dist(A) levels has
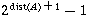 nodes,
so a general leftist tree of
nodes,
so a general leftist tree of
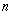 nodes (which might have nodes
dangling below the full levels) has:
nodes (which might have nodes
dangling below the full levels) has:
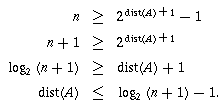
Since
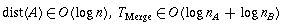 . If
. If
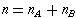 , then
, then
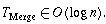
As a consequence, the running times of Insert and DeleteMin are
also in
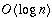 .
.