CSC418/2504F Fall 2002: Written Component of Assignment 3

1. [4 marks] A path is laid out for a car to follow using three Hermite curves.

1. [2 marks] If the road is to have G1 continuity, what property must the tangents of the curves have?  If the road is to have C1 continuity, what property must the tangents have?
2. [2 marks]  If the car is to drive along the path without veering off it, give an expression for the direction the car is facing at any time during the traversal.

2. [6 marks] Determine a parametric cubic curve defined by the following four points.

   P(0)   = P1
   P(1/4) = P2
   P(3/4) = P3
   P(1)   = P4

   Give the basis matrix, the basis functions, and sketch the basis functions.

3.  [5 marks]  Antialiasing

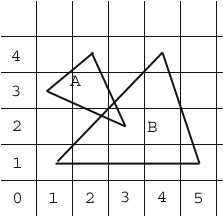
You are to rasterize two triangles using the A-Buffer.  When projected, triangle A has coords (1,3), (2,4) and (3,2), and triangle B has coords (1,1), (5,1) and (4,4) .  Triangle A is in front of B.  The background is white and has colour value 1.  Triangle A is Black and has colour value 0.  Triangle B is grey and has colour value 0.4.  The triangles are shown below.  Your answer should be the same grid, but indicate the pixel intensity value in each square.  Two decimal places of accuracy is fine.  A 4x4 sampling grid for each pixel should be used.