
Contour Chaining for Stroke Stylization
A Project in Non-Photorealistic Rendering
Download:
Contour Chaining (Win32, 1,131 kB)
Contour Chaining - Source Code (Win32, 12.9 MB)
Update February 16, 2018! Go to https://github.com/JamesMcCrae/ContourChainingQt for updated code on Github (based on Qt5, and removes GLUI/GLUT/DevIL/Vector class dependencies).
Overview:
The application lets one view renderings of a 3D triangular mesh in an illustrative style. To achieve this, it uses both the smooth contours of the mesh as defined in "Illustrating Smooth Surfaces" by Hertzmann and Zorin (SIGGRAPH '00) as well as suggestive contours as described in the paper "Suggestive Contours for Conveying Shape" by DeCarlo et al. (SIGGRAPH '03). Furthermore, the chains of line segments which constitute both types of contours are detected, and splines rendered with unique brush types can be fit along these chains to produce stylized strokes. Combined with toon shading, these elements form a system that quickly produces artistic renderings.
Features:
- Detection of visible mesh edge contours, smooth contours, and suggestive contours
- Toon shading
- Contour chaining to produce stylized strokes and abstract renderings
Images:
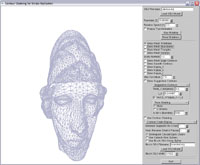
The "Atenea" mesh |
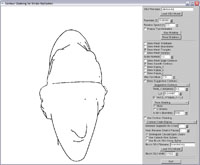
Smooth contours |
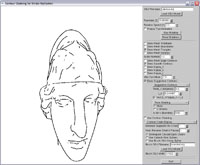
Smooth and suggestive contours |
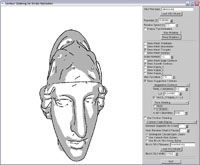
Toon shader applied |
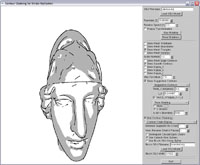
Fitting splines to
contour chains |
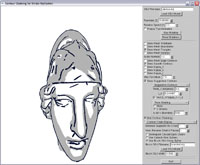
Fitting brush objects
along contour chains |
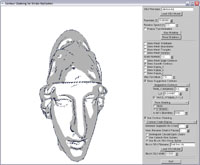
Using a "furry" brush object |
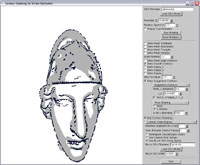
A helix-shaped brush object |
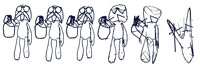
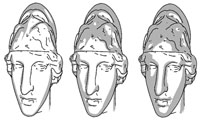
Master Rai, increasing the
number of reverse Chaikin
iterations can produce
abstract renderings |
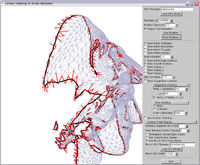
Showing mesh edge contours
(red) against smooth
contours (black) |
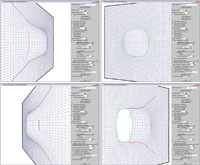
Contour chaining detecting
closed curves (green)
and open curves (red) |
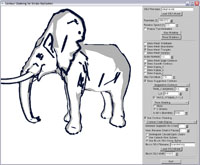
Elephant rendered using
brush object |

Bathroom Scene 1 |

Bathroom Scene 2 |
"Angela"
Contours Only |

"Angela"
Suggestive Contours |

"Angela"
Toon Shader |
Instructions:
- First load the mesh you wish to view. Enter the filename in the text box where it says "OBJ Filename" (default that works provided) and press the "Load OBJ Model" button.
- Left clicking and dragging the mouse allows you to change the viewpoint. Moving the mouse up and down zooms in and out, and left to right rotates the object.
- Checking the box labelled "Freeze Transformation" allows you to freeze the camera position. You can then change the viewpoint, yet view the mesh as if from the original camera position. All contours and toon shading are processed as if still in the original camera position.
- You can view the mesh in various ways, as well as its attributes, using many of the checkboxes on the right pane:
- Checking "Draw Mesh Wireframe" lets you view the edges of the mesh.

- Checking "Draw Mesh Boundaries" lets you view those edges that are at the boundaries of a mesh, which are present in the case the surface is not closed. They are drawn in black.
- Checking "Draw Mesh Triangles" (checked by default) draws a solid triangle for each face of the mesh. It uses OpenGL's Z-buffer to handle occlusion so parts of strokes that should be hidden, are in fact in the final rendering. Disabling this lets you see all of the contours of the mesh, occluded or not.

- Checking "Draw Mesh Normals" renders the normals of each vertex as line segments. A numeric spinner labelled "Scale Normals" allows you to scale the length of the rendered line segments.

- Checking "Draw Mesh Edge Contours" allows you to view the edges of the mesh which intersect the contours. These mesh edge contours will appear jagged as a result. They are rendered red. Using the "Freeze Transformation" feature makes it easier to see them (from a non-orthographic view).
- Checking "Draw Smooth Contours" (checked by default) draws the smooth contours of the mesh. The paths rendered are linearly interpolated from the mesh edge contours at the points where n dot v is equal to 0. They are rendered black.
- Checking "Draw kappa_1" renders the maximum principal curvature of the mesh, by colouring the triangles red. Checking "Draw kappa_2" renders the minimum principal curvature of the mesh, by colouring the triangles blue. The brighter the colour, the higher the curvature. Note that you can check both of these at the same time, and in areas where both the min and max principal curvatures are high, you'll see the regions as purple.

- Checking "Draw kappa_r" renders the radial curvature of the mesh, as calculated from the Euler formula for normal curvature from the principal curvatures. Red corresponds to positive curvature, blue to negative curvature. The brighter the colour, the greater the magnitude of the curvature. The intensity of the brightness for displaying the curvatures can be scaled using the "Max Curvature" spinner.

- Checking "Draw Suggestive Contours" (checked by default) calculates and draws the suggestive contours of the mesh. The panel labelled "Suggestive Contours" contains parameters that control how much of a suggestive contour is displayed. The "Theta_c" spinner culls line segments of the contour whose angular distance is less than this value (units in degrees). The "t_d" spinner is a constant of which the value D_w * kappa_r must be greater than in order to be displayed. This test can be enabled and disabled by checking and unchecking the box labelled "Test D_w*kappa_r>t_d" (checked by default).

- The radio group labelled "Toon Shading" lets you render the mesh with toon shading if desired. The spinner labelled "n dot v boundary" defines the boundary between the two shades. Note that the boundary between the shades is linearly interpolated along mesh edges, resulting in smooth shade boundaries rendered.
- Checking the box labelled "Use Contour Chaining" enables contour chain detection. Checking this feature allows you to do any of the following to the contours and suggestive contours:
- Cull entire contours based on the value in the spinner "Minimum Segments for Chain". The value is the minimum number of line segments that compose a chain (each line segment crosses a single face of the mesh, so the value is very much dependent on the number of faces in the mesh). It is useful for eliminating short, spurious contours.

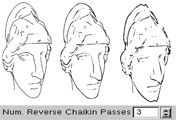
- The "Num Reverse Chaikin Passes" spinner sets the number of iterations of the reverse Chaikin (a reverse subdivision method) to apply to the set of points in the chain prior to fitting a spline curve. It reduces the number of control points in the curve by taking weighted local averages. Note that as the number of iterations of the reverse Chaikin method increases, the more the spline curve can deviate from the original contour. This can produce some interesting results, like progressively more abstract illustrations as the number of reverse Chaikin iterations increases.
- The "Distinguish Closed/Open Chains" radio button (selected by default) draws contours which are closed curves in green, and open curves in a gradient from black to red.

- The "Use Catmull-Rom Splines" radio button draws the Catmull-Rom spline (a C1 curve that passes through each point) that is fit to the chain. The "Num Reverse Chaikin Passes" value affects this mode of display.

- The "Use Brush OBJ Along Spline" radio button is a display mode which also fits a Catmull-Rom spline to the chain points, but in addition smoothly warps a brush object (another texture-mapped triangular mesh) along the spline. Since the brush object can be anything, this feature allows limitless variation in the resulting renderings. To load a particular brush object (in OBJ format), type the filename in the text area labelled "Brush OBJ Filename" (default that works provided) and press the "Load OBJ Model" button just below. You can interactively vary the thickness of the brush object using the "Brush OBJ Width" spinner. Again, the "Num Reverse Chaikin Passes" value has an affect when using this display mode.

- When finished, press the "Quit" button at the bottom of the right pane.
Implementation Details:
The project was implemented in C++. Libraries used include: OpenGL (graphics), DevIL (image processing), GLUI (user interface widgets), trimesh2 (for loading and processing triangular meshes). Uses a modified Vector class originally by Allen Sherrod.
The components of this project I implemented are:
- User interface - windows managed with GLUT, wrote OpenGL code for perspective projection, and set up the right pane that has all the widgets by manipulating objects from the GLUI library
- Code to determine:
- mesh edge contours - formed between vertices whose n dot v's have a sign change (one is negative, one is positive)
- smooth contours - linearly interpolating the point between vertices at which n dot v is zero, for two edges of each face. The smooth contours are formed by line segments which cross triangular faces.
- radial curvature - by using Euler's formula and the principal curvatures of the mesh (curvatures given by the trimesh2 library)
- suggestive contours - the line segments formed when the radial curvature kappa_r is 0 must be filtered such that the derivative of the curvature with respect to viewing direction is greater than 0 (curvature derivatives obtained using the trimesh2 library), and also that the angle made between the normal at that point of the contour and the viewing direction is greater than some threshold denoted theta_c
- the two-shade toon shader - the bounds of which again are linearly interpolated between vertices, the boundary between shades can be interactively changed by adjusting the threshold of the dot product between surface normal and viewing direction
- Data structure for contour chains - Created a data structure for chains (using STL objects) as well as a structure for a group of chains. To populate the chain group structure as quickly as possible, for those faces which are found to contain part of a contour, I immediately check the neighbouring faces to continue the contour chains. This is a speed improvement over the naive algorithm of just collecting all the contour line segments and trying to join the endpoints with any other (which is O(n^2)). As a result, the application runs at an interactive rate when using the contour chain feature for meshes containing a reasonable amount of faces.
- Spline interpolation - used a Catmull-Rom spline class I created from another project, to interpolate between the points of the chain. Also wrote the code to perform reverse subdivision process on the points.
- Warping brush object around spline - wrote the routine that takes a triangular mesh, and warps the vertices such that the follow the path of a spline. The Y-axis of the mesh corresponds to the arc-length position along each piece of the spline curve, and then X and Z are dimensions defined orthogonal to one another, and to the spline's tangent at Y.
















