1. Projection, drawing primitives: [8 marks] An
ellipse defined by semi-major and semi-minor axes vectors A, B is to be drawn using
orthographic projection with view direction V :
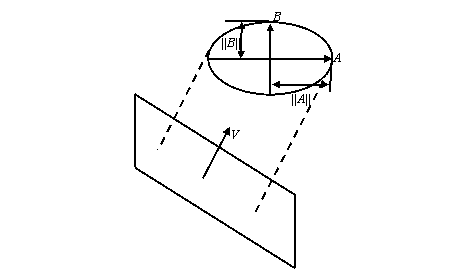
a.
[2 marks] Explain
intuitively why the projected curve must also be an ellipse or a straight line.
Possible answers (you will get partial credit for a reasonable attempt
at an answer):
The view space transform is a change of basis rotate and translate
transform that leaves an equation in x,y,z
to have the same or lesser degree. Orthographic projection sets z=0. A
quadratic thus projects to a quadratic or linear equation in x,y. If quadratic the ellipse
being closed projects to a closed quadratic that is an ellipse. (2 marks).
When (AxB).V=0 or the plane of the ellipse
is perpendicular to the view plane the curve projects to a line. (1 mark),
Ellipse eq. x=a*cost, y=bsint
z=0. Any view space rotation can be seen as a sequence of 3 rotation around x,y,z axes. Ignore rotation of
ellipse around z axes which is the projection plane (ellipse rotated in 2D is
an ellipse). After rotation around y by angle m, eq.
is x’=x, y’=ycosm, z’=xsinm. After rotation around y by angle n eq. is x’’ =xcosn
– xsinm*sinn,
y’’=ycosm , z’’=xsinn+xsinm*cosn. Throw away z’’ in the equation. We are
left with the projected curve x’’= a(cosn-sinm*sinn)cost,
y’’= b(cosm)sint
which is still the parametric eq. of an ellipse. (2 marks).
b.
[3 marks] Under what
conditions can the projected curve be a circle and what is the radius of that
circle as a function of A, B, V.
A’=sqrt(||A||2-(A.V) 2).
B’=sqrt(||B||2-(B.V) 2).
The curve is a circle when A’=B’=radius of the circle.
(1 mark for getting the A’, B’ values, 1.5 marks for saying
that when the new semi-maj, semi-minor axes are equal
we get a circle, 0.5 marks for pointing out that the radius is A’ or
B’.
c.
[3 marks] Write pseudo code
for a loop that plots the ellipse defined as (x/a)2 + (y/b)2 =1
as a sequence of n line segments.
ang=2pi(n-1)/n;px=a*cos(ang);py=b*sin(ang);
For (i=0;i<n;i++)
{ang=2pi*i/n; x=a*cos(ang);y=b*sin(ang); line(x,y,px,py);x=px;y=py;}
(1 mark for using the parametric eq.
of ellipse, 1 mark for loop str., 1 mark for getting
the angle incr. right). Same
marking scheme if you use the explicit equation for
4 quadrants.
d.
EXTRA CREDIT [2 marks] What property of the curve should determine where to sample
points on the ellipse so that the n
line segments that connect them best approximate the ellipse. What part of your
pseudo-code in part c needs to change
to reflect this.
The arc length of the ellipse between sample points should be roughly
equal for better approximation. Curvature of the ellipse can be used as a
measure of this. (1.5 marks). The angle increment is now not fixed but depends
on the arc length between samples (0.5 marks).
2.
Illumination: [8 marks]
Motion capture systems use a number of cameras, and spherical reflective
markers to track the position of the markers in time. The figure below shows
how it works. A marker reflection needs to be picked up by 2 or more cameras.
Given the position of the camera and reflected spot in the camera image, the
viewing ray for the camera is determined. Now the 3D position of the marker is
the intersection point of the two viewing rays.
P Y
![]()

![]()
Camera1
X![]()
![]()
![]()
![]()
Camera2 Z
a. [2 marks] Why are the markers spherical in shape and reflective?
We want the markers
to show up in the camera images as sharp spots irrespective of the relative
angles between the lights, marker and cameras. They are spherical in shape so
that they reflect well in all directions and they are reflective so that they
show up as
sharp highlights in the camera images.
(1 mark for
spherical, 1 mark for reflective).
b. [4 marks] Two cameras positioned at <0,0,0> and <1,0,7> pick
up a marker and their view rays are calculated to be directed along <1,1,2> and
<2,3,-1> respectively. What is the position of the 3D surface point P
captured by this setup?
<1,1,2>s = <1,0,7> + <2,3,-1>t. s=1+2t, s=3t, 2s=7-t =>
t=1, s=3, P=<3,3,6> .
(1 mark for writing
the ray equation. 1 mark for equating them. 1 mark for solving s or t. 1 mark for getting P
right).
c. [2 marks] Typical motion capture systems have many more than 2 cameras
spread around in the scene to track the motion of markers. Why?
When objects move,
the markers are not always visible to all cameras. If we have more than two
cameras the chance that a marker is picked up by at least 2 of the many cameras
becomes higher with more cameras.
d. EXTRA
CREDIT [2 marks] If view vectors V1..Vn
for a marker are calculated for n cameras in the scene how will you
calculate the 3D marker position?
Calculate pairwise intersections for all Vi
and Vj, Set the point to be the average of these
intersection points. …or calculate shortest distance between view vectors
and take the midpoint of the shortest distance line as the intersection point
if they don’t intersect. Weight average the intersection points based on
the shortest distance between the view vectors.
3.
Visibility: [10 marks] Consider a set of polygons, represented in 2D cross-section
as line segments. Arrows represent front-facing normals.
![]()
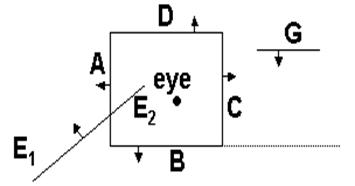
a. [4 marks] Draw the BSP
tree obtained by inserting the polygons in alphabetical order. Left subtrees correspond to the front side, and right subtrees to the back. If any polygons are split, label the
fragments on the diagram and the tree.
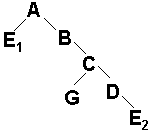
(partial credit for getting parts of the tree right).
b. [4 marks] Consider a drawing primitive, represented as the hatched
region in the figure below, of a cylinder (defined by center C,
axis A,
radius r and height h with no caps) and a plane with origin O and normal N
such that N.A=0. Give the equations
and the test by which one may determine if a point P is on one side of the
primitive or the other, similar to the planar equation test for polygons in a BSP.
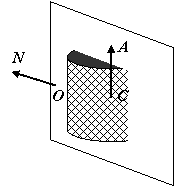
For the point to be on the front side of hatched region it must be in
front of the plane and outside the cylinder. i.e.
plane:
(P-O).N>0
cylinder:
let d=(P-C).A. d’= sqrt((P-C).(P-C)-d2). d’>r
Front/back side test is:
(P-O).N>0 and d’>r.
(2 marks for saying front of plane and outside cyl., 1 mark for plane eq. test., 1 mark for cyl.
outside test).
c.
[2 marks] Describe any
changes needed to the BSP algorithm to adapt it to be
used as visibility ordering algorithm for the partial-cylinder primitive above.
Replace the planar equation test with the test in part b. When primitives intersect use a clipping algorithm that
clips to both the plane and the cylinder so that the resulting pieces are all
on one side or another.
(1 mark each for pointing out the two changes).
4.
True or False with a reason:
[4 marks]
a.
[1 mark] The difference
between Gouraud and Phong
shading is likely to be more noticeable with diffuse objects than with specular objects.
False. Specular objects tend
to be more sensitive to changes in normal vector on the surface than diffuse
objects.
b.
[1 mark] The difference
between Gouraud and Phong
shading is likely to be more noticeable with large polygons than with small
polygons (size of the polygon here is its projected size in the 2D image).
True. It is more likely to miss specular
highlights on large polygons with Gouraud shading
than on small polygons.
c.
[1 mark] Real cameras use a
lens to compensate for the fact that apertures larger than a pin-hole make the
image blurry.
True. Lenses cause rays through the aperture to focus towards a smaller
region on the image plane making the image sharper.
d.
[1 mark] The result of
multiple rotations to a point is order dependent but combinations of scaling
and translations can be applied in any order with the same result.
False. Take a point at the origin and scale it 2x and
translate it to (5,5).
If translated and then scaled the resulting point is (10,10).