CSC418/2504F Fall 2003: Midterm Test:
Wednesday, Nov. 5,
2003 , 7:00 PM
Family Name:_____________________________
First Name:
_____________________________
Student ID:
_____________________________
Instructions:
Attempt
all questions.
There
are four questions.
The
total mark is 30.
You have 50 minutes to complete the test.
Aids
allowed: Calculators (you should not need one).
Textbooks
and notes are NOT allowed.
1:
/8
2:
/8
3:
/10
4:
/4
_________
Total: /30 + 4 extra credit
1. Projection, drawing primitives: [8 marks] An
ellipse defined by semi-major and semi-minor axes vectors A, B is to be drawn using
orthographic projection with view direction V :
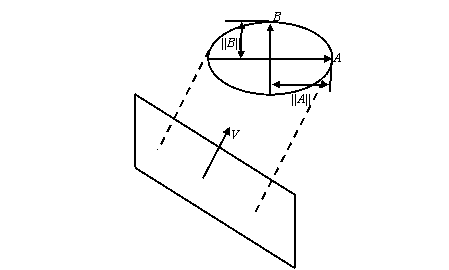
a.
[2 marks] Explain
intuitively why the projected curve must also be an ellipse or a straight line.
b.
[3 marks] Under what
conditions can the projected curve be a circle and what is the radius of that
circle as a function of A, B, V.
c.
[3 marks] Write pseudo code
for a loop that plots the ellipse defined as (x/a)2 + (y/b)2 =1
as a sequence of n line segments.
d.
EXTRA CREDIT [2 marks] What property of the curve should determine where to sample
points on the ellipse so that the n
line segments that connect them best approximate the ellipse. What part of your
pseudo-code in part c needs to change
to reflect this.
2.
Illumination: [8 marks]
Motion capture systems use a number of cameras, and spherical reflective markers
to track the position of the markers in time. The figure below shows how it
works. A marker reflection needs to be picked up by 2 or more cameras. Given
the position of the camera and reflected spot in the camera image, the viewing
ray for the camera is determined. Now the 3D position of the marker is the
intersection point of the two viewing rays.
P Y
Camera1
X
Camera2 Z
a. [2 marks] Why are the markers spherical in shape and reflective?
b. [4 marks] Two cameras positioned at <0,0,0> and <1,0,7> pick
up a marker and their view rays are calculated to be directed along <1,1,2> and
<2,3,-1> respectively. What is the position of the 3D surface point P
captured by this setup?
c. [2 marks] Typical motion capture systems have many more than 2 cameras
to track the motion of markers. Why?
d. EXTRA CREDIT [2 marks] If view vectors V1..Vn for a marker are calculated
for n
cameras in the scene how will you calculate the 3D marker position?
3.
Visibility: [10 marks] Consider a set of polygons, represented in 2D cross-section
as line segments. Arrows represent front-facing normals.
a. [4 marks] Draw the BSP
tree obtained by inserting the polygons in alphabetical order. Left subtrees correspond to the front side, and right subtrees to the back. If any polygons are split, label the
fragments on the diagram and the tree.
b.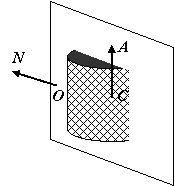 
[4 marks] Consider a drawing primitive, represented as the intersection
(hatched region in figure below) of a cylinder (defined by center C,
axis A,
radius r and height h with no caps) and a plane with origin O and normal N such
that N.A=0. Give the equations
and the test by which one may determine if a point P is on one side of the
primitive or the other, similar to the planar equation test for polygons in a BSP.
c.
[2 marks] Describe any
changes needed to the BSP algorithm to adapt it to be
used as visibility ordering algorithm for the partial-cylinder primitive above.
4.
True or False with a reason:
[4 marks]
a.
[1 mark] The difference
between Gouraud and Phong
shading is likely to be more noticeable with diffuse objects than with specular objects.
b.
[1 mark] The difference
between Gouraud and Phong shading
is likely to be more noticeable with large polygons than with small polygons
(size of the polygon here is its projected size in the 2D image).
a.
[1 mark] Real cameras use a
lens to compensate for the fact that apertures larger than a pin-hole make the
image blurry.
b.
[1 mark] The result of
multiple rotations to a point is order dependent but combinations of scaling
and translations can be applied in any order with the same result.