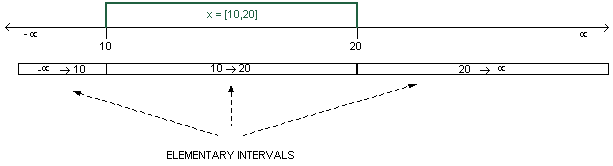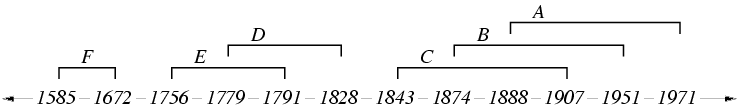We would store them in an interval tree. This is an augmentation
of the BST data structure.
An interval tree has a leaf node for every elementary interval. On
top of these leaves is built a complete binary tree. Each internal
node of the tree stores, as its key, the integer that separates the
elementary intervals in its left and right subrees. The leaf nodes do
not store any keys, and represent the elementary intervals. In the
interval tree below, the key is shown in the top of each node.
How would we store the actual (non-elementary) intervals in this tree?
Each node of the tree (both internal nodes and leaf nodes) can
store a set of intervals. In the tree above, this set is
shown in the bottom of each node.
We could store these sets as linked lists. Each leaf (which
corresponds to an elementary interval) would contain a pointer to a
list of non-elementary intervals that span the leaf's elementary
interval. For example:
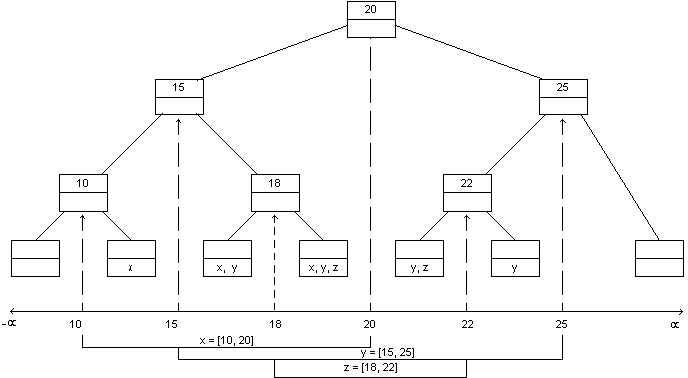
What's wrong with this picture?!
It uses up too much space: If each interval were very long, it
could potentially be stored in every leaf. Since there are n
leaves, we are looking at O(n2) storage!
So how do we improve the storage overhead?
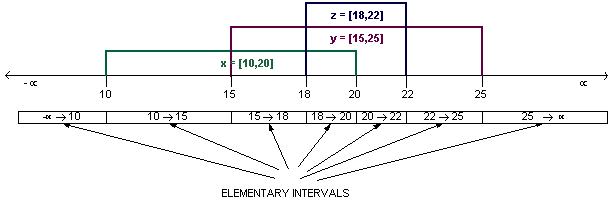
An internal node is said to ``span'' the union of the
elementary intervals in its subtree. For example, node 18 spans the
interval from 15 to 20: In other words: span(18) = [15,20].
Suppose that, rather than store an interval in each individual
leaf, we will store it in the internal nodes. Here is the rule:
An interval [a,b] is stored in a node x if and only if
- 1)
- span(x) is completely contained within
[a,b] and
- 2)
- span(parent(x)) is not
completely contained in [a,b].
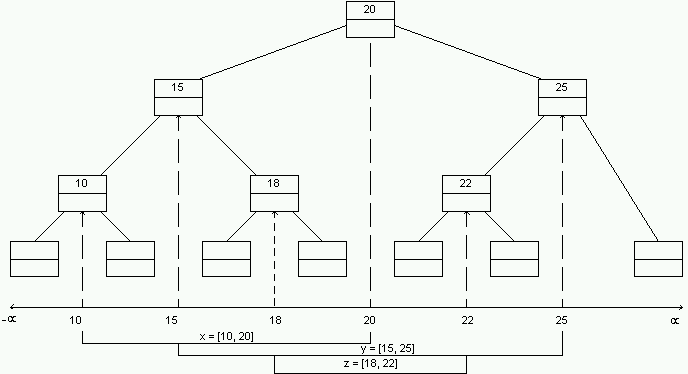
Let's incorporate this rule into our tree:
Each interval can be stored at most twice at each level. (Can you
prove this?)
This gives us O(n log n) storage - actually 2 n log
n, which has a very low coefficient.
MUCH BETTER!
A More Complex Example
Suppose we have a set of composers and their lifespans; each
lifespan is an interval of years between the composer's birth and
death. The following table gives an example.
| Interval |
Composer |
Birth |
Death |
| A |
Stravinsky |
1888 |
1971 |
| B |
Schoenberg |
1874 |
1951 |
| C |
Grieg |
1843 |
1907 |
| D |
Schubert |
1779 |
1828 |
| E |
Mozart |
1756 |
1791 |
| F |
Schuetz |
1585 |
1672 |
The intervals are shown on the integer line. Each interval is
labelled with a letter corresponding to one of the composers in the
table:
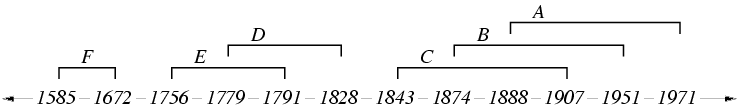
Notice that the endpoints a and b of each interval
[a,b] divide the integer line into elementary
intervals. The elementary intervals for the composers are:
[-infty,1585], [1585,1672], [1672,1756], [1756,1779], ...,
[1907,1951], [1951,1971], [1971,+infty].
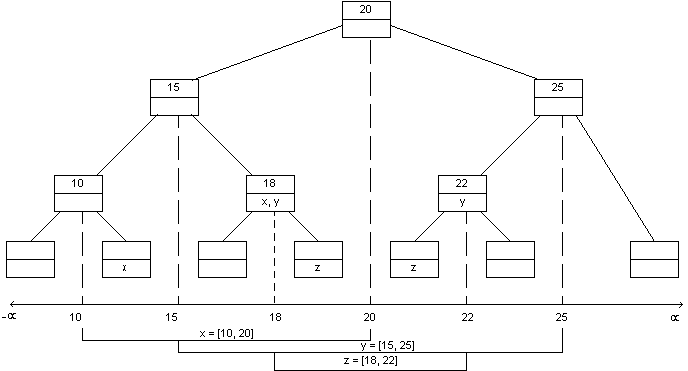
Here is the Interval Tree for our composers:
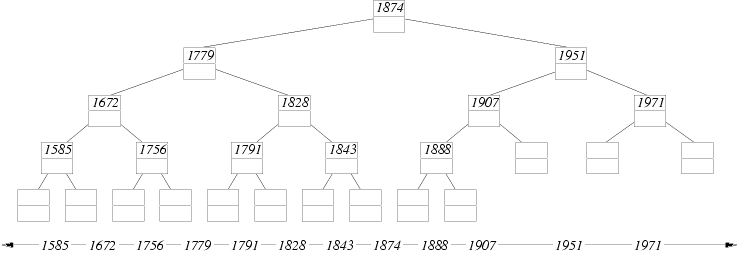
Notice that node 1828 spans the four elementary intervals between 1779
and 1874. In this case, we say span(1828) =
[1779,1874]. A leaf node spans only one elementary interval.
And here's the tree with the intervals stored in each node according
to the rule above:
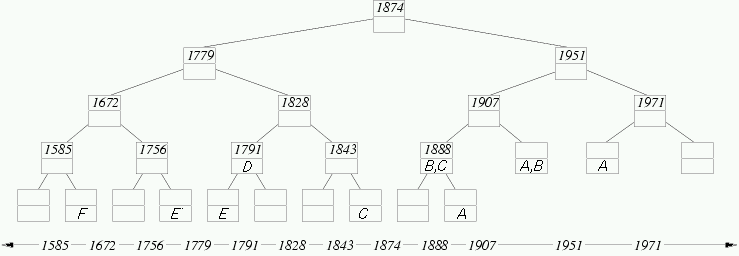
For example, the interval C = [1843,1907] corresponds to
Grieg's lifetime. This interval is stored in node 1888
because
- 1)
- span(1888) = [1874,1907] is completely
contained within [1843,1907] and
- 2)
- span(parent(1888)) = [1874,1951] is
not completely contained within [1843,1907].
The interval C is also stored in the leaf node to the right
of 1843 because this node also satisfies conditions (1) and (2).
Test your understanding:
Suppose interval G = [1672,1779]. Which nodes in the tree
above would contain a G? Hint: Start by adding
G to each elementary node spanned by [1672,1779]. This
satisfies condition (1) above. However, if G is in both
children of a node x, then condition (2) is not satisfied
by the children because the span of their parent,
span(x), contains G. Whenever this
occurs, remove G from each child and add it to the parent,
x. Repeat this until G cannot be moved upward anywhere
in the tree.
Try another: In the tree above, write an H in each
node that stores the interval [1756,1971].
Storage cost: Each interval can be stored in many nodes of
the tree. However, the conditions (1) and (2) ensure that any
particular interval is stored in at most two nodes on each level of
the tree.
Given this information and the fact that a tree of n
intervals has O(n) leaf nodes, what is an asymptotic upper
bound on the space required to store the n intervals inside the
tree nodes? Assume that an interval requires O(1) space for
each node in which it is stored.
How do we answer queries of the form ``What composers were alive in
such-and-such a year?'' For example, the composers alive during 1910
were Stravinsky (A) and Schoenberg (B).
In the abstract, the query algorithm must do the following: Given
an integer k and an interval tree T, list all the
intervals stored in T that contain k. An interval
[a,b] contains k if a <= k <= b.
The query algorithm must simply enumerate the intervals stored in
the leaf that contains k. It must also enumerate the
intervals stored in internal nodes whose span includes k.
These are the ancestors of the leaf that contains k. So the
query algorithm simply follows a root-to-leaf path to find the leaf
corresponding to the elementary interval containing k, and
enumerates all the intervals stored in nodes on that root-to-leaf
path.
Each node stores the usual left and right
pointers. In addition, it stores separator, which is the
value that separates elementary intervals in its left and right
subtrees. It also stores intervals, which is a pointer to a
linked list of the intervals.
/* listIntervals( k, x )
*
* List all the intervals that contain k in the subtree rooted at x.
*
* This is intitially called as listIntervals( k, root ).
*/
listIntervals( k, x )
while x != NULL
output intervals(x)
if k < separator(x)
x = left(x)
else
x = right(x)
endif
endwhile
Here the problem is to add [a,b] to the tree, assuming
that the endpoints a and b are already in the tree; that
is, a and b already separate elementary intervals
somewhere in the tree.
Essentially, we've got to descend from the root just until
we find a node x whose span is completely contained in
[a,b]. Then rule (1) is satisfied. At this point we store
the interval in x and stop. Note that rule (2) is satisfied
at x because we didn't stop at x's parent
(otherwise we wouldn't have reached x). Also note that we're
guaranteed to stop at a leaf.
But if we reach a node x whose span is not completely
contained in [a,b] we simply recurse into each subtree of
x that contains any part of [a,b]. We know that
condition (1) is not satisfied at x, but that it will be
satisfied at some of x's descendants.
/* addInterval( I, a, b, min, max, x )
*
* The interval to insert is [a,b] and is named I. We assume that the
* values a and b separate elementary intervals somewhere in the tree.
* [min,max] is the span of the current subtree rooted at node x.
*
* This is initially called as addInterval( I, a, b, -infinity, +infinity, root ).
*/
addInterval( I, a, b, min, max, x )
if a <= min and max <= b
/* span(x) is completely within [a,b], so store the interval and stop */
store I in intervals(x)
else
/* span(x) contains some elementary intervals that aren't in [a,b].
* We must recurse until we find a subtree that is completely contained
* in [a,b]. Note that we might recurse into both subtrees. */
if (a < separator(x))
addInterval( I, a, b, min, separator(x), left(x) );
endif
if (separator(x) < b)
addInterval( I, a, b, separator(x), max, left(x) );
endif
endif
How long do this algorithm take in a tree of n elementary
intervals? The reasoning to answer this is not obvious.