Next: 2.15.2 Cauchy Sequences
Up: 2.15 Real Representations
Previous: 2.15 Real Representations
A real number 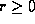 is represented by a cut
is represented by a cut 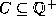 ,
,
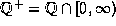 .
Every cut has the property that for all
.
Every cut has the property that for all 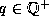 :
:
As presented, the cut 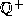 represents
represents
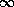 . Disallowing this
special cut gives a representation for all non-negative real numbers.
In general,
Most numbers have a
representation that cannot be written out directly since
the representation is an infinite set.
. Disallowing this
special cut gives a representation for all non-negative real numbers.
In general,
Most numbers have a
representation that cannot be written out directly since
the representation is an infinite set.
Operations on reals are inherited from the corresponding
operations on rationals. For example, a binary operation on two
real numbers, represented by cuts X and Y,
is given by:
Difficulties are encountered when generalizing this to
negative real numbers. If a cut is simply redefined to
be a subset of 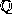 , then
the product of two cuts is not a cut if the
multiplicands correspond to negative numbers.
, then
the product of two cuts is not a cut if the
multiplicands correspond to negative numbers.
See [8, 64] for further details concerning this representation
and associated methods.
Next: 2.15.2 Cauchy Sequences
Up: 2.15 Real Representations
Previous: 2.15 Real Representations
![]() is represented by a cut
is represented by a cut ![]() ,
,
![]() .
Every cut has the property that for all
.
Every cut has the property that for all ![]() :
:
![]()
![]()
![]()