Given the binary function ![]() ,
let
,
let ![]() and
and ![]() denote
unary functions, for any
denote
unary functions, for any ![]() .
These functions are one-dimensional slices of g,
for a constant x or constant y.
The functions are defined as follows:
.
These functions are one-dimensional slices of g,
for a constant x or constant y.
The functions are defined as follows:
We now restrict our attention to grid functions. The function g is a grid function if it is defined over a grid:
![]()
![]()
A grid function ![]() may be classified using the scheme set out
for unary functions:
may be classified using the scheme set out
for unary functions:
![]()
![]()
![]()
An upper bound for ![]() , where
, where ![]() ,
is determined by considering
,
is determined by considering ![]() , for all
, for all ![]() ,
and then
,
and then ![]() , for a particular
, for a particular ![]() .
Since
.
Since ![]() , the same
, the same ![]() produces an upper bound
of
produces an upper bound
of ![]() . Exceptional functions,
whether they are partial, discontinuous or bumpy, are handled as before.
For g, where
. Exceptional functions,
whether they are partial, discontinuous or bumpy, are handled as before.
For g, where ![]() :
:
![]()
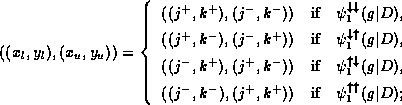
| Jeff Tupper | March 1996 |