Next: 2.8 Real Interval Arithmetic
Up: 2.7 Interval Arithmetic
Previous: 2.7.4 Interval Extension
Intervals generalize floating point numbers since there
is an injective mapping 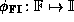 defined by:
defined by:
This mapping is not an isomorphism, although it allows one
to identify the floating point numbers
with 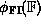 .
The mapping
.
The mapping 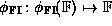 defined by:
is an isomorphism between
defined by:
is an isomorphism between 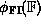 ,
a subset of the intervals, and
,
a subset of the intervals, and 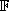 .
A mapping
.
A mapping 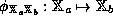 is an isomorphism if
is an isomorphism if 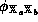 is a homomorphism
from
is a homomorphism
from 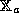 to
to 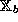 , and
, and 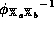 is a homomorphism from
is a homomorphism from 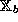 to
to 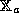 .
.
Addition inherits the identity 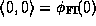 while multiplication inherits the identity
while multiplication inherits the identity 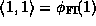 .
Since intervals were constructed with mathematical rigor
in mind, several nice properties are obeyed by intervals.
Chief among these is the sub-distributive law:
.
Since intervals were constructed with mathematical rigor
in mind, several nice properties are obeyed by intervals.
Chief among these is the sub-distributive law:
Although neither addition nor multiplication are associative,
the operators preserve ``associative trails''.
This property is expressed, for addition, as follows:
The property follows from the associativity of
real addition and the inclusion property of interval addition.
The above property can be extended by considering that
interval addition is commutative.
In general, a real computation result is guaranteed to be
contained in the result of the associated interval computation because
the interval inclusion property is transitive.
Next: 2.8 Real Interval Arithmetic
Up: 2.7 Interval Arithmetic
Previous: 2.7.4 Interval Extension
![]() defined by:
defined by:
![]()
![]()
![]() while multiplication inherits the identity
while multiplication inherits the identity ![]() .
Since intervals were constructed with mathematical rigor
in mind, several nice properties are obeyed by intervals.
Chief among these is the sub-distributive law:
.
Since intervals were constructed with mathematical rigor
in mind, several nice properties are obeyed by intervals.
Chief among these is the sub-distributive law:
![]()
![]()